

El teorema de Thales nos permitirá encontrar segmentos proporcionales sin necesidad de conocer sus medidas.
 |
r correspondiente s |
|
| AB | DE | |
| AC | DF | |
| BC | EF | |
|
TEOREMA: AB/AC=DE/DF AC/BC=DF/EF AB/BC=DE/EF |
||
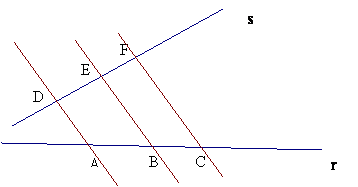
"Si dos rectas r y s del plano se cortan por varias rectas paralelas, la razón de dos segmentos cualesquiera de una de ellas es igual a la razón de los segmentos correspondientes en la otra. Los segmentos que se determinan en una de ellas son proporcionales a sus correspondientes en la otra recta."
| Empezaremos dibujando los segmentos AB y CD iguales, al trazar por los extremos de los segmentos, rectas paralelas entre si, cortarán a la otra recta, determinando en ella dos segmentos, EF y GH que también serán iguales. | ||
| ACTIVIDADES: | ||
| a) Comprueba que hemos dibujado iguales los segmentos AB y CD, pinchando con el ratón en el punto A y arrastrando hasta C. Pulsa inicio. | ||
| b) Se trazan AP y CQ
paralelos a la recta s e iguales a EF y GH, respectivamente, por formar un
paralelogramo. Compruébalo (pincha en P y arrastra hasta F, pincha en H y
arrastra hasta Q). Pulsa inicio. VAS a comprobar que los triángulos ABP y CDQ son iguales, pinchas en Q y arrastras hasta P. Esto es así porque los triángulos tienen iguales los lados AB y CD y los ángulos adyacentes a ellos ,por correspondientes entre paralelas (A=C y B=D). |
||
| c) Luego AP = CQ y por tanto EF= GH . | ||
Para demostrar el teorema de Thales, nos queda estudiar qué ocurre si los segmentos AB y CD no son iguales.
|
ACTIVIDAD: Tienes que elegir la medida de los segmentos
AB y CD, para ello la escribes y pulsas ENTER o bien utilizas las flechas. A
continuación pulsas animar. ¿Qué ocurre? Los segmentos se dividen en segmentos iguales según su medida. Habrá tantos segmentos iguales en la otra recta como segmentos iguales haya en la primera. |
||
| Por lo tanto AB/CD = EF/GH | ||
|
Se puede generalizar para cualquier par de
segmentos, por ej.: AC/AB = EG/EF |
Segmentos - Proporcionalidad de segmentos - Teorema de Thales - Aplicaciones del teorema de Thales - Longitud de una circunferencia
|
|||||||||||||||