

LA LONGITUD DE UNA CIRCUNFERENCIA
I.-Teorema.- Dos circunferencias son proporcionales a sus radios.
Sean c y C las longitudes de dos circunferencias cuyos radios son r y R.
|
ACTIVIDAD:
1.- Traslada la circunferencia de centro A, trasladando el punto A hasta el punto B. Necesitamos dibujar dos polígonos regulares inscritos en estas circunferencias, escoge el número de lados (k) y pulsa animar. Si p es el perímetro del polígono regular inscrito en la circunferencia c y P es el perímetro del mismo polígono inscrito en la circunferencia C, por la semejanza de estos polígonos tendremos que: P/p =R/r |
|
|
Ahora bien. creciendo indefinidamente el número de lados de ambos polígonos, pero teniendo uno y otro el mismo número de lados, ¿qué le pasa a la razón de los perímetros? |
|
|
¿Podemos afirmar que C/c = R/r=2R/2r? ¿Cómo se deduce que C/R =c/r? |
|
2.- Deduce que la razón de la circunferencia al diámetro es constante
Sabemos que la razón de la circunferencia al diámetro es constante. Porque si:
C/c = R/r = 2R/2r , entonces C.2r = c.2R y de aquí deducimos que: C/2R = c/2r.
Representando esta razón por la letra griega π (pi), será C/2R = π.
La longitud C de la circunferencia es C=2πR.
Idea acerca del cálculo de π: El número π (pi), es la relación de la circunferencia al diámetro: π = C/2R.
Vamos a dibujar una circunferencia. si consideramos que su diámetro es la una unidad, será 2R=1(unidad), C=π(unidades) y R = 1unidad/2. Siendo, por tanto, el número π igual a la longitud de una circunferencia cuyo radio es igual a 1unidad/2.
| ACTIVIDAD:
Pulsa ANIMAR Considerando el exágono regular inscrito, como hizo Arquímides, se tendrá: Lado del exágono=Radio Perímetro del exágono: p= 6.1/2=3unidades |
|
| Duplicando cinco veces el número de lados resultará un polígono inscrito cuyo perímetro es p5=3,14145unid. El perímetro del correspondiente polígono circunscrito es P5=3,14188unid. | |
| Luego el valor aproximado por defecto del número π será 3,14145 con tres cifras decimales exactas. |
|
| ¿Cuántos lados tienen los polígonos que se obtienen duplicando los lados de un exágono? ¿Cuántos lados tienen los polígonos citados, p5 y P5? . Intenta dibujarlos, para ello cambias el valor de k (número de lados) y pulsas animar. | |
FÓRMULAS QUE PERMITEN CALCULAR A PARTIR DEL LADO DE UN POLÍGONO INSCRITO, LOS PERÍMETROS DE LOS POLÍGONOS: INSCRITO DE DOBLE NÚMERO DE LADOS, CIRCUNSCRITO Y CIRCUNSCRITO DE DOBLE NÚMERO DE LADOS.
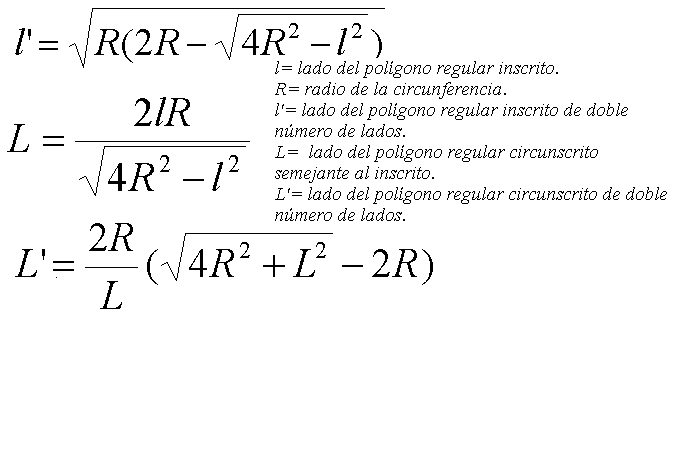
La proporción que existe entre las longitudes de las circunferencias y sus radios nos permite establecer una correspondencia entre ángulos y arcos.
ACTIVIDAD 1:
|
¿Tienen
igual longitud los arcos de cada circunferencia marcados en rojo? ¿Se corresponden con el mismo ángulo CENTRAL? Pulsa ANIMAR Si varías k, cambias la longitud de todos los arcos en función del radio respectivo. k=nº de radios Si varías r dibujas circunferencias de radio r unidades. Si cambias r o k pulsa después ENTER |
" Si el arco dibujado tiene la misma longitud que el radio, el ángulo central correspondiente se denomina RADIÁN".
ACTIVIDAD 2: Pulsa inicio - Cambia el valor de r, por ej: r = 3 - Ahora vas a calcular la longitud del arco correspondiente a la circunferencia de radio r unidades en los siguientes casos k=1, 2.5 y 4 - Utiliza la figura para comprobar si lo has hecho bien y pulsa animar en cada caso.¿Qué ángulos se van dibujando?(en radianes) - ¿Qué valor tiene que tener k para que el ángulo central sea de 360º?¿Cómo se denominará?
Segmentos - Proporcionalidad de segmentos - Teorema de Thales - Aplicaciones del teorema de Thales - Longitud de una circunferencia
|
|||||||||||||||