

APLICACIONES DEL TEOREMA DE THALES
Dos triángulos se llaman semejantes cuando tienen sus ángulos respectivamente iguales y los lados homólogos proporcionales.
Se llaman lados homólogos a los lados opuestos a ángulos iguales.
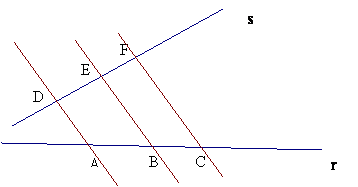 |
En este dibujo, los triángulos ABC y DEF son semejantes. | |
| Ángulos iguales: | Lados homólogos: | |
| D = A | EF y CB | |
| E = B | DF y AC | |
| F = C | DE y AB | |
| Los lados homólogos son proporcionales: | ||
|
EF/CB =DF/AC = DE/AB |
||
"Toda recta paralela a un lado de un triángulo, que no pase por el vértice opuesto, y que corte a los otros dos lados o a su prolongación, determina un nuevo triángulo semejante al propuesto."
ACTIVIDAD: Mueve el punto A y observa los triángulos que se forman.
La recta BD es paralela a la recta AC. Estas rectas cortan a las rectas 0B y OD, lo que nos permite aplicar el teorema de Thales. Por eso decimos que: OB/OA =OD/OC. Si queremos demostrar que los triángulos OAC y OBC son semejantes, tendremos que demostrar que: BD/AC =OB/OA =OD/OC.
|
ACTIVIDAD: Pulsa animar, ahora hemos trazado una recta paralela al lado OD, lo que nos permite aplicar de nuevo el teorema de Thales desde otro punto de vista. Utilizaremos los lados OB y BD. |
| ¿Qué pasa con los segmentos PD y AC? |
| ¿Qué pasa si comparamos la razón de los segmentos BD y PD con la de los segmentos OB Y OA o con la de los segmentos OD Y OC? ¿Qué deduces? |
II.- Semejanza de polígonos regulares.
Se llama polígono regular todo polígono convexo que tiene sus lados iguales y sus ángulos también iguales.
Dos polígonos regulares de igual número de lados se llaman semejantes cuando tienen sus ángulos respectivamente iguales y los lados homólogos proporcionales.
El teorema visto en el punto I, nos permite afirmar que todos los polígonos regulares de igual número de lados son semejantes
| ACTIVIDAD: Con esta escena comprobaras que se cumple para un pentágono. Mueve el punto A, centro del polígono pequeño hasta el centro del polígono grande. | |
| ¿Cómo son los triángulos? | |
|
¿Qué relaciones se cumplen entre los lados de los triángulos? |
|
La relación entre dos polígonos regulares de igual número de lados es:
L / l =R / r = ap /aap
|
ACTIVIDAD:
1.-Vas a dibujar varios polígonos regulares de 5, 6 y 9 lados. Pulsa inicio, sólo tienes que cambiar el valor de k, utilizando las flechas o escribiendo directamente su valor (en este caso tienes que pulsar ENTER después de escribir el número deseado). Pulsa animar para ver el polígono. Pulsa inicio para volver a empezar. 2.- Traslada el punto A hasta el punto B (pinchas con el ratón y arrastras) y repite el ejercicio anterior. Al empezar no te olvides de pulsar inicio |
|
¿Cómo son los triángulos dibujados? |
|
Escribe la igualdad de razones correspondiente a esta figura |
|
¿ Se pueden cambiar la relación para expresarla así: L / R =l / r o bien L /ap = l /ap ? |
| En cada polígono los lados son iguales, ¿se puede decir que: P / R=p / r ?.(p y P son los perímetros de los polígonos? |
|
3.- Pulsa inicio, aumenta el valor de k, por ejemplo haz k=23 y después pulsa animar, repite para K=36. ¿A qué se aproxima el polígono? |
Segmentos - Proporcionalidad de segmentos - Teorema de Thales - Aplicaciones del teorema de Thales - Longitud de una circunferencia
|
|||||||||||||||