Inversas de las funciones radicales.
Análisis (ampliación)
 

Inversas de las funciones radicales.

Ya hemos visto en la primera escena de la página anterior que las funciones radicales son inyectivas. Trataremos ahora de comprender cuáles son sus funciones inversas. Antes de empezar, ¿cuál crees que va a ser la función inversa de la raíz cúbica? ¿y de la raíz cuadrada? Veamos con detenimiento qué sucede porque la situación no es tan obvia como parece al principìo.

En primer lugar familiarízate con la escena. Observa que en esta ocasión se dibujan dos funciones para cada valor de n. Una de ellas, la negra, es la función radical de índice n, la roja es la función potencia f(x)=(s*x)n . 

Observa que cuando n es par la función f(x)=(s*x)n es la misma independiente mente de que s valga 1 o -1. Sin embargo, si n es impar la función no es la misma. Por ejemplo, para n=2 obtenemos como función roja f(x)=x2  tanto para s = 1 como para s = -1. Pero para n


Ejercicio 11: Escribe la forma simplificada de la función roja cuando n=3 y s=-1. Haz lo mismo para s=1 y n=5 y para  s=-1 y n=4. Reproduce la gráfica de alguna de estas tres funciones en u cuaderno observando la escena y realizando una tabla de valores.
Recordemos que las funciones cuadráticas no son inyectivas. Observando la función roja segun los valores de n comprueba que sucede lo mismo con todas las potencias de grado par, sin embargo, con las de grado impar no sucede lo mismo, éstas son inyectivas.

Si queremos calcular la inversa de una función cuadrática sucede los siguiente: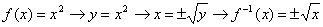

Lo que quiere decir que si x es positiva la inversa de f(x)=x2  es la raíz cuadrada positiva. Mientras que si x es negativa la inversa  es la raíz cuadrada negativa. En resumen:

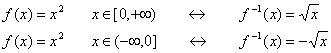
Observa haciendo n=2, modificando el valor de s que esta situación se traduce  gráficamente a la escena. Cuando s=1 la rama derecha de la parábola es la inversa de la radical, mientras que si s=-1 es la rama izquierda la que es inversa de la radical. Observa también que esta situación se mantiene para todos los valores pares de n. 

Ejercicio 12: Calcula las inversas de las funciones radicales de índice 4 haciendo un estudio análogo al del caso 2. Apóyate en la escena para hacerlo. Haz dos gráficas una con la función radical positiva y su inversa y otra con la radical negativa y su inversa.

El caso de las funciones radicales de índice impar es más sencillo. Calculemos la inversa de f(x)=x3 (función inyectiva).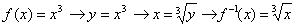



Observa haciendo n=3 en la escena comprueba el hecho que acabamos de explicar. Modificando el valor de s comprueba que para s=-1 la situación es análoga. Comprueba que para los demás valores impares de n la situación es análoga que para n=3. 


Ejercicio 13: Describe de forma general las inversas de las funciones radicales de índice impar según sean positivas o negativas. Realiza la gráfica de la función radical y su inversa para el caso n=3 s=-1. 

Para calcular la inversa de una función radical trasladada como las de la segunda escena tenemos que fijarnos en la posición del vértice. Comprueba que en la escena puedes cambiar las fórmulas de las funciones que se dibujan. Ensaya primero a dibujar varias funciones de esta forma y utiliza este hecho para comprobar la solución de los siguintes ejercicios:

Ejercicio 14: ¿Cual es la función inversa de f(x)=(x-1)1/3 ? 

Ejercicio 15: ¿Cual es la función inversa de f(x)=(x)1/2 +2? 



  Sergio Martínez Juste
 
Ministerio de Educación, Cultura y Deporte. Año 2009.