Funciones radicales (primeras propiedades)
Análisis (ampliación)
 

Hemos aprendido anteriormente a calcular dominios de forma algebraica para funciones del tipo:

       

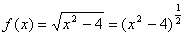
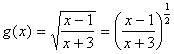
 Ejercicio 1: Elige alguna de las dos funciones anteriores y calcula su dominio.

En esta sección aprenderemos a dibujar las gráficas de algunas de estas funciones, estudiaremos sus propiedades y las relacionaremos con las fuciones polinómicas.

Gráfica y propiedades.

En primer lugar, estudiaremos las gráficas de las funciones radicles básicas, aquellas del tipo f(x)= x1/n (función radical de índice n). NOTA: A partir de ahora utilizaremos la expresión exponencial en vez de dibujar el símbolo de los radicales.

En la escena se muestra inicialmente la gráfica de la función f(x)=x1/2.Puedes cambiar el valor del índice con el control situado en la parte superior derecha de la escena. Para desplazarte por la escena puedes usar los controles para el eje X y eje Y y el zoom.

Puedes desplazar el punto P por la gráfica de la función. En la parte inferior se muestra el valor de las coordendas de este punto con una precisión de decimales que puedes modificar según convenga.

Familiarízate con la escena y después contesta a los ejerccios que se proponen.

Observa que la forma de la gráfica, y por tanto, las propiedades de las funciones radicales, depende esencialmente de la paridad del índice. Por tanto, habrá que distinguir entre funciones radicales con índice par y funciones radicales con índice impar. 

Ejercicio 2: Calcula ayudándote de la escena las siguientes raíces con una aproximación de 2 decimales.
  1. Raíz cuadrada de 6.
  2. Raíz cúbica de -12.
  3. Raíz sexta de 9'3.
Ejercicio 3: Encuentra al menos 5 puntos con coordenadas enteras que estén sobre la gráfica de la raíz cuadrada y otros cinco sobre la de la raíz cúbica. Ayúdate de ellos para copiar la gráfica en tu cuaderno con la mayor exactitud posible.

Ejercicio 4: Para n=2 y n=3 describe: Dominio, recorrido, intervalos de crecimiento y decrecimiento, máximos y mínimos, continuidad e inyectividad.

Ejercicio 5: Generaliza los resultados del apartado anterior para describir las propiedades de las funciones radicales según n sea par o impar.
Funciones radicales trasladadas.

En este apartado vamos a analizar cómo, a partir de la gráfica de una función radical como las estudiadas en la escena anterior, podemos obtener nuevas funciones radicales que son meras traslaciones de las anteriores (recuerda que hicimos este estudio para las funciones hiperbólicas). En resumen, trataremos de describir las funciones radicales del tipo:

f(x)= (x-a)1/n  + b                  y                    f(x)= - (x-a)1/n + b

Vamos a explicar en qué consiste la escena: en ella se representa la función: 

f(x)=s*(x-a)1/n  + b 

Donde s puede tomar el valor 1 o -1. Compruébalo modificando el control signo en la parte inferior de la escena. De esta manera podemos dibujar las dos funciones que hemos anunciado. (Observa cómo cambia la gráfica según los valores de s).

Sobre la gráfica hemos resaltado un punto al que hemos llamado P. Este punto se llama vértice de la función radical. Observa que es el punto donde comienzan las funciones con índice par y es un punto carácterístico de las de índice impar. Las coordenadas de este punto se destacan en la parte inferior izquierda de la escena.

Observa detenidamente la forma en la que se desplaza la función al cambiar el valor de los parámetros a y b. Observa también cómo se invierte al cambiar el valor de s. No te olvides de ir cambiando el índice para estudiar las distintas funciones radicales. 

Recuerda que con la expresión anterior las funciones a las que hacemos referencia son aquellas de la forma:

 

Ejercicio 6: ¿Qué relación existe entre las coordenadas del vértice y los parámetros a y b?

Ejercicio 7: Ayudándote de lo trabajado en la anterior escena y dibujando la gráfica en esta nueva escena estudia las propiedades de la función obtenida haciendo a = 3   b = 2   s = -1   n = 2. (No te olvides de escribir la fórmula de la función con estos valores).

Ejercicio 8: Como en el anterior para los valores a = -2'4    b = -1    s = 1   n = 3.

Ejercicio 9: ¿Qué influecia tiene el valor de s en las propiedades de las funciones radicales de índice impar?

Ejercicio 10: ¿Qué influencia tienen los valores a y b en las propiedades de las funciones radicales de índice par?


       
         
  Sergio Martínez Juste
 
Ministerio de Educación, Cultura y Deporte. Año 2009