
Existencia de la derivada
Derivadas laterales
¿Por qué usamos las derivadas laterales?
Quizás te haya pasado desapercibido que, en todos los ejemplos utilizados, la función estaba definida a ambos lados del punto x=a.
Esto no siempre es así
Vamos a ver otro ejemplo de una función que no está definida a la izquierda o a la derecha de algún punto. Se trata de la función y=0.5x2 definida en el intervalo cerrado [0,2]. Por tanto a la izquierda de x=0 no está definida, y a la derecha de x=2 tampoco.
Recordarás que en el estudio de continuidad de funciones se hablaba de los límites laterales para distinguir si nos acercamos a un número por la derecha o por la izquierda. Vamos a usar la idea de límite lateral para definir dos números que ya hemos tenido que utilizar sin ponerles nombre.
| 1.- Recorre la curva en
[0,2] arrastrando P con el ratón. Fíjate en lo que
aparece en la escena para familiarizarte con ella. 2.- Sitúate en el punto a=0 y elige un punto a su derecha modificando el valor de h. Sólo puedes dar valores positivos porque a la izquierda no hay función. Observa cómo varían las TVM para h>0 y acercándose a cero. Si h=0 aparece la derivada por la derecha. No tiene sentido acercarse por la izquierda porque no hay función. NO TIENE DERIVADA 3.- Sitúate en a=2 y elige ahora puntos a su izquierda (h<0) Ahora h no puede ser positivo porque la función no existe a la derecha de 2. Si h=0 aparece la derivada por la izquierda.No tiene sentido acercarse por la derecha porque no hay función.NO TIENE DERIVADA 4.- Elige otro punto y acércate a él dando a h valores positivos para ver la derivada por la derecha, y negativos para ver la derivada por la izquierda. Para h=0 aparecen las dos derivadas y coinciden. TIENE DERIVADA |
Derivadas laterales
Se llama derivada lateral por la derecha de la función y=f(x) en x=a al límite de las tasas de variación media cuando nos acercamos a "a" por la derecha, esto es con h>0.

Se llama derivada lateral por la izquierda de la función y=f(x) en x=a al límite de las tasas de variación media cuando nos acercamos a "a" por la izquierda, esto es h<0
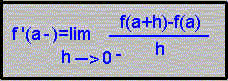
Algunas veces la derivada no existe
Es posible que hayas supuesto que las funciones tienen derivada en los puntos que no sean extremos. De hecho la mayoría de las funciones que definimos con una fórmula van a ser derivables en casi todos los puntos de su dominio.
Vamos a insistir en aquellas que tienen puntos en los que la derivada no existe.
Ahora vas a ver un ejemplo con una función que tiene un punto especial al estudiar la derivada. Aparentemente esta función no debería ser distinta de las anteriores, se trata de dos semirectas que nos resultan muy familiares, es y=IxI
Fíjate en la siguiente escena:
| 1.-
Localiza en la gráfica el punto x=2
2.- Elige valores de h positivos y cada vez más pequeños usando las flechas del parámetro h y observa el valor de la TVM en la escena. Anota tus conclusiones y da un valor a la derivada por la derecha 3.- Elige valores de h negativos aproximándose a 0 y observa el valor de la TVM. Da un valor a la derivada por la izquierda 4.- Comprueba que estos límites laterales no coinciden, por tanto la función NO ES DERIVABLE en x=2 5.- Sin embargo sí ES DERIVABLE en el resto de los puntos.Prueba para a=3 y a=1 |
Una función tiene derivada en un punto cuando las derivadas laterales coinciden en ese punto.
Has visto que al pasar por algunos puntos la tasa de variación media puede cambiar su valor bruscamente. Esta es la razón por la que el punto es anguloso.
Pues bien, en esos puntos no existe la derivada y sin embargo se puede observar alguna regularidad si la estudiamos separadamente a la derecha o a la izquierda del punto.
Las funciones cuya gráfica presenta puntos angulosos no son derivables en esos puntos.
Nueva definición de la derivada
Se llama derivada de una función en el punto x=a al límite, cuando exista, de la expresión:

Es importante que tengas en cuenta el hecho de que la derivada existe si las derivadas laterales coinciden en el punto. Esto significa que la TVM cambia suavemente (puntos suaves). Las secantes se aproximan a la recta tangente si nos acercamos a P haciendo que h se aproxime a 0.
Por el contrario, si las derivadas laterales no coinciden, esto es la TVM cambia bruscamente, entonces la derivada no existe (puntos angulosos). En este caso tampoco existe la recta tangente ya que según nos acercamos por la derecha o por la izquierda aparecen dos rectas tangentes distintas y tendríamos que referirnos a la tangente por la derecha o la tangente por la izquierda.
Mira esta escena y observa atentamente lo que ocurre. Se trata de una función definida en dos tramos usando una parábola convexa y otra cóncava.
1.- Sitúate en el punto a=1 y elige valores de h cada vez más pequeños usando las flechas. Fíjate en la evolución de las TVM y en las rectas secantes que van dejando rastro. ¿Sabrías dar un valor a la derivada por la derecha? 2.- Repite el acercamiento desde h=-1 tomando valores negativos que se acerquen a cero. Fíjate en el valor de las TVM y en las secantes. ¿Sabrías cuanto vale la derivada por la izquierda? 3.- Haz h=0 con el teclado y verás las derivadas laterales, la recta tangente y el valor de la derivada si existen. 4.- Repite las comprobaciones en a=2 y observarás algo diferente |
Has visto un nuevo ejemplo de una función con un punto anguloso.En x=2 la función no tiene derivada ya que las derivadas laterales, aunque existen, no coinciden.
Sin embargo en el resto de los puntos la función sí es derivable. Puedes volver a la escena, poner h=0 y arrastrando con el ratón ir viendo dónde existe la derivada y por tanto la tangente a la función.
Teorema importante. Relación con la continuidad
Si una función es derivable en x=a, entonces es contínua en x=a
Este teorema se demuestra fácilmente usando las propiedades de los límites.
Nosotros vamos a recurrir a su contrario para entender lo que ocurre.
Si f no es contínua en x=a, f no puede ser derivable en x=a
Observa que esta afirmación nos va a permitir rechazar algunos puntos cuando queramos estudiar la derivabilidad de una función.
En la siguiente escena vas a ver reflejada esta situación.
| 1.- Sitúate en x=3. esta
función tiene un salto en x=3. Es discontínua. 2.- Fíjate en el valor que toma la TVM para h=1, h=0.1, h=0.01, h=0.001, h=0.0001. ¿Cuánto vale la derivada por la derecha? 3.- Teclea h=-1, h=-0.1, h=-0.01, h=-0.001, h=-0.0001 y observa la evolución de las TVM. ¿Cuánto vale la derivada por la izquierda en x=3?. Como ves la TVM aumenta extraordinariamente al acercarnos a P. La secante se va poniendo vertical. 4.- Esta función no es derivable en x=3, no tiene derivada por la izquierda. |
Acabas de ver un ejemplo de una función discontinua y que no tiene una derivada lateral (por la izquierda). La función está definida en todos los puntos pero la discontinuidad de salto no deja que exista esa derivada lateral.
Si la discontinuidad es evitable no existen ninguna de las derivadas laterales.
En la siguiente página verás este caso.
El teorema recíproco no es cierto
Una función continua puede no ser derivable
De hecho ya sabes reconocer aquellos puntos en los que, a pesar de ser continua, la función no va a tener derivada. Son esos puntos angulosos que ya has visto en la segunda escena.
Ya que la TVI ha de variar bruscamente han de ser puntos en los que la gráfica presenta un pico más o menos suavizado. Si te imaginas las tangentes a la curva puedes reconocer fácilmente ese cambio brusco.
En la página siguiente verás que hay otros puntos en los que la gráfica no tiene picos y tampoco va a existir la derivada
CONCLUSION
La derivada de una función y=f(x) en un punto x=a es la pendiente de la tangente a la curva en ese punto y nos mide la velocidad con que cambia y respecto de x en ese punto, es decir, la tasa de variación instantánea.
Para que exista la derivada de y=f(x) en x=a debe cumplirse:
1.- La función es continua en x=a
2.- Existen las derivadas laterales ( son números reales)
3.- Estas derivadas son iguales y su valor es la derivada de f en x=a.
| Ministerio de Educación, Cultura y Deporte. Año 2000 | ||
Autor: Rosa Jiménez Iraundegui