Otros ejemplos
Relación entre continuidad y derivabilidad. Discontinuidad evitable
Teníamos pendiente estudiar el comportamiento de la derivada en las discontinuidades evitables.
Vamos a ver otro ejemplo de una función que tiene en x=2 una discontinuidad evitable. La función es
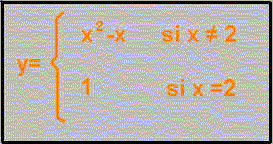
| 1.- Recorre la curva
arrastrando P con el ratón. Fíjate en lo que aparece en
la escena para familiarizarte con ella. Observa la
discontinuidad evitable 2.- Sitúate en el punto a=2 y elige un punto a su derecha modificando el valor de h. Observa cómo varían las TVM para h>0 y acercándose a cero. Si h=0 la secante se convierte en una recta vertical. La DERIVADA POR LA DERECHA ES MAS INFINITO. 3.- Sitúate de nuevo en a=2, elige ahora puntos a su izquierda (h<0) y observa la evolución de las TVM. Si h=0 la secante se convierte de nuevo en una recta vertical. LA DERIVADA POR LA IZQUIERDA ES MENOS INFINITO 4.- Esta función NO ES DERIVABLE en x=2 y NO EXISTE TANGENTE en ese punto. 5.- Elige otro punto y acércate a él dando a h valores positivos para ver la derivada por la derecha, y negativos para ver la derivada por la izquierda. Para h=0 aparecen las dos derivadas y coinciden. LA FUNCION ES DERIVABLE Y EXISTE TANGENTE en cualquier otro punto. |
Las funciones con discontinuidad evitable no son derivables en los puntos de discontinuidad ya que las derivadas laterales son infinitas. En estos puntos la tangente no existe, las secantes evolucionan hacia una recta vertical que pasa por la discontinuidad.
Derivadas laterales infinitas. Caso1
Veamos la función 
Se trata de una función que es continua en todos los puntos. Vamos a fijarnos con atención en el punto de abscisa x=0
Fíjate en la siguiente escena:
| 1.-
Localiza en la gráfica el punto x=0. Esta función es
contínua en este punto. 2.- Fíjate en el valor que toman las derivadas laterales y la derivada en a=1, a=0.1, a=0.01, a=0.001, a=0.0001.Esta función es derivable en todos esos puntos pero el valor de la derivada crece desmesuradamente al aproximarnos a cero. Esta función en a=0. NO TIENE DERIVADA POR LA DERECHA PORQUE ES INFINITA 3.- Repite el proceso para a=-1, a=-0.1, a=-0.01, a=-0.001, a=-0.0001 y observa la evolución de las derivadas. Crecen muy deprisa al acercarnos a a=0. NO TIENE DERIVADA POR LA IZQUIERDA PORQUE DE NUEVO ES INFINITA 4.- Fíjate en la evolución de las rectas tangentes al acercarnos a a=0. Son rectas que se van poniendo verticales 5.- Esta función NO ES DERIVABLE en x=0 porque las derivadas laterales, aunque coinciden, SON INFINITAS. 6.- La función NO TIENE TANGENTE en x=0. |
La función raiz cúbica de x es continua en todos los puntos pero no tiene derivada en x=0 (es infinita). No existe la tangente, las secantes evolucionan hacia una recta vertical que pasa por x=0 ( el eje de ordenadas).
Esta situación se va a producir cuando la función sea continua y tenga un punto de inflexión cóncavo-convexo si la función es creciente o convexo-cóncavo si la función es decreciente.
Derivadas laterales infinitas. Caso 2
Veamos otra función continua que tampoco es derivable.
Se
trata de la función 
Fíjate en la escena:
1.- Sitúate en el punto a=1 y elige valores de a cada vez más pequeños como en la escena anterior. Fíjate en la evolución de las derivadas y en las rectas tangentes. 2.- Repite el acercamiento desde a=-1 tomando valores negativos que se acerquen a cero. Fíjate en el valor de las derivadas y en las tangentes. 3.- En a=0 La función NO TIENE DERIVADA PORQUE LAS DERIVADAS LATERALES QUE SON INFINITAS TIENEN ADEMAS DISTINTO SIGNO. NO EXISTE TANGENTE 4.- En el resto de los puntos sí es derivable y existe la recta tangente. |
La
función es continua pero no es
derivable en x=0 porque las derivadas laterales son infinitas y
de distinto signo. No existe la tangente, las secantes
evolucionan hacia una recta vertical que pasa por x=0 (eje de
ordenadas).
La tangente sí atraviesa a la curva
Veamos un nuevo ejemplo. Se trata de una función que SI tiene TANGENTE y ésta atraviesa la curva.
En la siguiente escena vas a ver reflejada esta situación. Se trata de la función y=x3
| 1.- Esta función es
contínua en todos los puntos. Sitúate en a=0 2.- Fíjate en el valor que toma la TVM para h=1, h=0.1, h=0.01, h=0.001, h=0.0001. ¿Cuánto vale la derivada por la derecha? 3.- Teclea h=-1, h=-0.1, h=-0.01, h=-0.001, h=-0.0001 y observa la evolución de las TVM. ¿Cuánto vale la derivada por la izquierda en x=0?. 4.- Como ves la tangente se va poniendo horizontal. 5.- Esta función sí es derivable en x=0, f´(a)=0 y la tangente es horizontal y atraviesa la curva |
Observa que esta situación se va a repetir siempre que la curva sea continua y tenga un punto de inflexión que puede ser convexo-cóncavo si la función es creciente o cóncavo-convexo si la función es decreciente.
 |
||
| Ministerio de Educación, Cultura y Deporte. Año 2000 | ||
Autor: Rosa Jiménez Iraundegui