Esta es una fórmula de Descartes. De hecho es una escena de Descartes, como el lector puede comprobar haciendo un doble clic sobre ella. Escribir una fórmula como ésta es muy fácil usando el editor de fórmulas de Descartes. Este editor permite escribir fórmulas elementales de cualquier grado de complejidad y Descartes las puede presentar en sus escenas.
El editor de fórmulas.
Las fórmulas en Descartes no existen independientemente de los textos sino como parte de ellos. Para crear una fórmula hay que crear un texto y en el editor de textos se pueden insertar fórmulas. (Una fórmula pura es un texto que lo único que tiene es una fórmula.)
El editor de texto siempre inserta la misma fórmula: 1+x, pero las fórmulas pueden modificarse fácilmente. Para ello basta hacer un doble clic sobre una fórmula en el editor de textos y con ello aparecerá el editor de fórmulas mostrando la fórmula seleccionada a punto para ser modificada.
Esta es una imagen del editor de fórmulas:
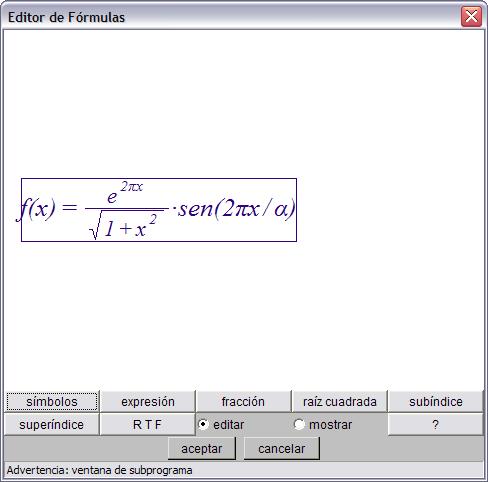
Al centro aparece la fórmula rodeada por un rectángulo. Abajo aparecen varios botonos e interruptores cuya función se explica más adelante.
Para acceder a una parte de la fórmula basta hacer un clic del ratón en el sitio donde se desea poner el cursor de texto. El resultado es que quedará enmarcada en un rectángulo la parte a la que se accedió y el cursor de texto quedará colocado lo más cerca posible del sitio del clic. Por ejemplo si en la fórmula de la imagen de arriba hacemos un clic en la letra pi que aparece en el exponente del numerador de la fracción, la ventana del editor queda así:
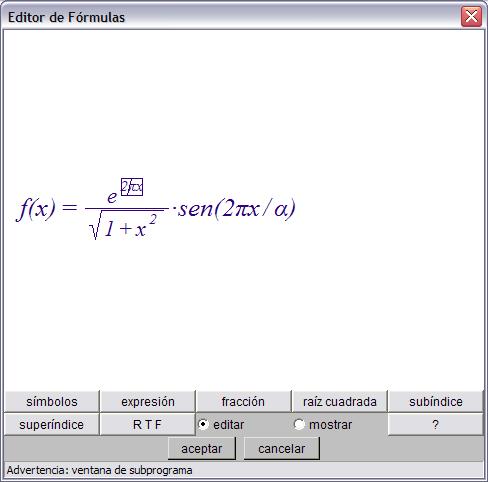
En cualquier momento se pueden escribir letras usando el teclado o insertar símbolos usando el botón símbolos que abre la tabla de símbolos. También en cualquier sitio se pueden insertar una expresión, una fracción, una raíz cuadrada, un subíndice o un superíndice pulsando uno de los botones con estos nombres.
La inserción de una expresión aparece como [expr] encerrado en un rectángulo. La imagen de abajo muestra una fórmula donde hay varias expresiones insertadas, todas ellas se muestran como [expr] encerrado en un rectángulo.
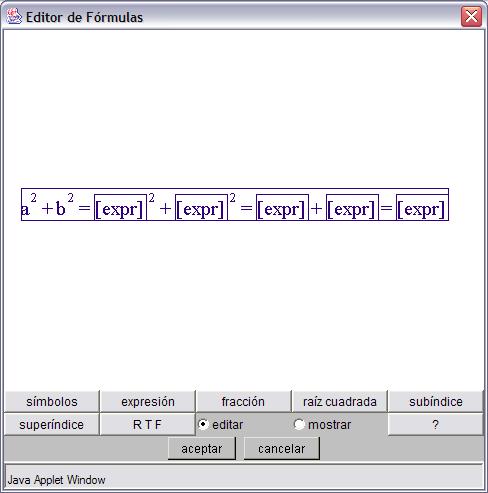
En realidad "detrás" de cada una de estas [expr] encerradas en rectángulos hay una expresión. Para acceder a ella hay que hacer un doble clic sobre el rectángulo. Por ejemplo al hacer un doble clic sobre el último rectángulo aparece el editor de expresiones:
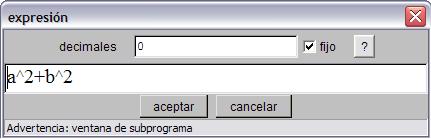
En este caso la expresión es a^2+b^2. Cuando se inserta una expresión nueva ésta siempre es x y para modificarla hay que abrir (con un doble clic) el editor de expresiones y modificarla allí. Esta expresión se evaluará y el resultado de la evaluación se escribirá con el número de decimales especificado y en formato fijo o ajustado de acuerdo con el interruptor.
En el campo decimales hay que escribir el número de decimales (máximo) con el que se presentará el resultado de evaluar la expresión. Si no se especifica (es decir, si se deja en blanco) entonces se usará el valor de decimales heredado del objeto gráfico.
El interruptor fijo determina si el número de decimales es fijo o se usa formato ajustado eliminando los ceros innecesarios a la derecha del punto decimal. La elección sólo es válida si el número de decimales no se deja en blanco pues cuando el número de decimales se deja en blanco se usa el valor de fijo heredado del objeto gráfico.
La inserción de cualquier otro objeto: fracción, raíz cuadrada, subíndice o superíndice da como resultado que aparece el objeto con un valor por defecto que luego puede modificarse borrando e insertando caracteres y otros objetos. A continuación se explican las características de cada inserción particular.
-
fracción: Botón que inserta u na fracción. La fracción que se inserta siempre es 1/2.
El tamaño de los caracteres del numerador y denominador se reducen a (9/10) un 85% del tamaño correspondiente a la parte donde se inserta la fracción.También see puede arrastrar este elementoal texto activo. -
raíz cuadrada: Botón que inserta una raíz cuadrada o de cualquier índice. El tamaño de los caracteres del índice a 4/5 del correspondiente a la parta donde se inserta.El radicando de la raíz que se inserta es siempre 2.El tamaño de los caracteres del radicando no se reduce.También se puede arrastrar este elemento al texto activo.
-
subíndice: Botón que inserta un subíndice.El subíndice que se inserta siempre es 1.
El tamaño de los caracteres del subíndice es (4/5) 66.7% del correspondiente a la parte donde se inserta.También se puede arrastrar este elemento al texto activo. -
superíndice: Botón que inserta una portencia ( o superíndice):El superíndice que se inserta siempre es 2. El tamaño de los caracteres del superíndice es de ( 4/5) 66.7% del correspondiente a la parte donde se inserta. También se puede arrastar este elemento al texto activo.
- sumatoria: Botón que inserta una suma o sumatoria.El tamaño de los caracteres de los límites inferior y superior se reduce a 4/5 del correspondiente a la parte donde se inserta.El tamaño de los caracteres del sumando no se reduce.También se puede arrastrar este elemento al texto activo.
- integral: Botón que inserta una integral definida.El tamaño de los caracteres de los límites inferior y superior se reduce a 4/5 del correspondiente a la parte donde se inserta.El tamaño de los caracteres del integrando no se reduce.También se puede arrastrar este elemento al texto activo.
- expresión. Botón que inserta una expresión para ser evaluada.En modo de edición todas las expresiones se muestran con la palabra 'expr' encerrada en un rectángulo.Cuando el texto no está en modo de edición, las expresiones se evalúan y lo que se muestra es el resultado: un número en formato decimal.Para editar el contenido de la expresión hay que hacer un doble clic sobre ella, lo cual abre un cuadro de diálogo con una ventana que permite editar la expresión y definir el número de decimales con que se escribirá el resultado, y si la representación decimal es fija o ajustada.La expresión que se inserta por defecto es '1'.También se puede arrastrar este elemento al texto activo.