|
1. INFORMACIÓN
EXTRAÍDA DE LA FUNCIÓN
|
|
1)
Dominio
2) Cortes con los
ejes y signo de f(x)
-
Con el eje OY:
hacemos x=0 en la fórmula de la función y calculamos el valor de y
resultante.
-
Con el eje
OX:
aquí debe ser y=0, luego resolvemos la ecuación f(x)=0
-
Estudiar
el SIGNO de f(x) puede servirnos para determinar las regiones donde
se dibujará la gráfica. Consideramos los intervalos
determinados por los puntos de corte con el eje OX y los puntos de
discontinuidad si los hubiera, y estudiamos el signo de la función
en cada uno de ellos.
|
|
|
|
Dando
a función valor 1, se dibujará una función y=f(x). Cambiando el valor de x
ó arrastrando el punto rojo con el ratón podrás ver los valores
que toma |
-
Escribe
el dominio de la función de la figura
-
¿En
qué puntos corta a los ejes coordenados?
-
¿En
qué intervalos f(x)>0?, ¿dónde es f(x)<0?
| Utiliza
el botón LIMPIAR, después da
a función valor 2, se dibujará otra función y=g(x) |
|
|
3) Simetría y
periodicidad
-
Una
función y =f(x) es PAR si
f(-x)=f(x). En este caso la gráfica es
simétrica respecto al eje de ordenadas
-
Una función
y=f(x) es IMPAR si f(-x)=-f(x). En este caso es simétrica respecto al origen.
-
Una función
es PERIÓDICA de periodo P si
f(x+P)=f(x). Su gráfica se repite
cada cierto intervalo de amplitud P.
|
|
|
-
Da
a función valor 1, comprueba, cambiando el valor de la
x ó arrastrando el punto rojo con el ratón, que la función que se dibuja es
IMPAR. Observa la simetría respecto al origen.
|
|
4) Asíntotas
-
VERTICALES:
Si
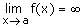 la recta
x=a es asíntota vertical.
-
HORIZONTALES:
Si
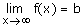la recta y=b es asíntota horizontal.
-
OBLICUAS:
Cuando
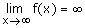puede haber asíntota oblícua, la recta y=mx+n, donde
|
|
|
-
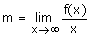
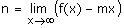
Observa
la función de la escena. Comprueba,
cambiando el valor de x, que cuando x®-1
y cuando x®1,
y®¥.
¿Cuáles son
las asíntotas verticales?.
¿Qué ocurre cuando x®¥
ó
cuando x®-¥?,
| Utiliza
el botón LIMPIAR, después da
a función valor 1, se dibujará de nuevo y=f(x). Cambia
el valor de x o arrastra el punto rojo. |
|
