INICIACIÓN AL CÁLCULO DE DERIVADAS. APLICACIONES
Optimización - Necesidad de las derivadas
El problema de la lata de aceite
Supongamos que tenemos que diseñar una lata de
aceite en forma de cilindro y que tiene
que contener un litro (1000 cm3) de aceite. ¿Cuáles son las
dimensiones que debe tener la lata, de manera que requiera la mínima cantidad
de metal para su manufactura?
Supongamos que utilizamos las letras r y h para
representar el radio y la altura (medidas ambas magnitudes en centímetros) el
volumen V será expresado:
V=πr2h
Que si debe ser de 1000 cm3 nos
lleva a la relación: 1000=
πr2h
Solo podemos determinar una de las
dimensiones de la lata, ya que si escogemos un cierto valor para el radio la
altura queda determinada por la relación anterior siendo la ecuación que la
identifica la siguiente:
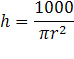
Para poder usar la mínima cantidad de metal
posible, debemos buscar el radio que de la lata de aceite cuya superficie de
contorno sea mínima. Suponiendo láminas uniformes en grosor y calidad de
material
Área
de la superficie = área de la tapa + área del fondo + área lateral
Área
de la superficie = πr2+ πr2+ 2 πrh
Área
de la superficie = πr2+ πr2+ 2πr(1000/πr2)
Hemos de considerar que r es una variable
sujeta a ciertas restricciones físicas, no puede ser cero ni negativa, pero a
pesar de ello todavía nuestro problema tiene un número ilimitado de posibles
soluciones.
1.-
Observa que, manteniendo el volumen constante, puedes variar el radio y cambia
la forma y la superficie que contiene a ese volumen.
Simplificando y llamando S a la superficie
anterior hemos establecido la siguiente función que la relaciona con el radio.
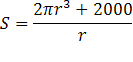
2.-En tu cuaderno dibuja una tabla para los
siguientes valores y expresa el volumen en dm3 para que sea más
fácil su representación.
|
Radio
(cm) |
Área
(dm3) |
|
2 |
|
|
3 |
|
|
4 |
|
|
5 |
|
|
6 |
|
|
7 |
|
|
8 |
|
3.- Observa los puntos en la gráfica
siguiente:
4.- Observa que aunque la tabla no contiene
probablemente la solución del problema, al menos nos ayuda para hacer una
aproximación a la curva, que obtenemos representando la función obtenida.
¿Podrías dar una solución aproximada? Compárala con la de tus compañeros.
5.- Observa que lo que necesitamos encontrar para resolver el problema es el
punto más bajo de la gráfica. La primera coordenada de este punto más bajo, es
la elección exacta del radio r que
da por resultado la lata de aceite de área mínima, mientras que la segunda
coordenada proporciona el valor numérico del área de la superficie.
Problema de la caja
De un cartón rectangular de 4x5 decímetros hacemos una caja sin tapa; para lo cual recortamos cuadrados de igual tamaño en las cuatro esquinas del cartón y doblamos las cejas con el fin de formar los lados. Nuestro objetivo es construir una caja con el mayor volumen posible.
V = (5-2x)(4-2x)x
6.- Observa que necesitamos
saber el punto más alto de la curva que es donde está la solución del problema.
7.- Observa que el punto más
alto de la curva se encuentra justamente donde la curva termina de ascender,
aunque todavía no haya empezado a descender. ¿Qué ángulo forma con la
horizontal la recta tangente a la gráfica que describe ese punto en ese
momento?
|