Semejanza de triángulos

SEMEJANZA DE TRIÁNGULOS.

TEOREMA FUNDAMENTAL DE LA SEMEJANZA.

Semejanza de triángulos.

Toda figura poligonal puede descomponerse en trángulos, por ello el estudio de la semejanza en los triángulos adquiere tanta impostancia. Dos triángulos, al igual que cualquier par de figuras, van a ser semejantes si tienen la misma forma. Esta condición se traduce de manera matemática relacionando sus lados y sus ángulos.

Dos triángulos son semejantes si cumplen:

1. Sus lados son proporcionales:

dichos cocientes representan la razón de semejanza.

2. Sus ángulos respectivamente son iguales: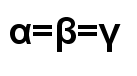

Esta unidad interactiva requiere la máquina virtual de Java J2RE.

1.- Modifica la posición de los vértices del triángulo azul ¿Son siempre paralelos los lados de ambos triángulos?

Teorema Fundamental de la semejanza.

Si tenemos dos triángulos ABC y A´B´C´ con un ángulo común y los lados opuestos a ese vértice son paralelos, podemos situarlos de tal forma que el triángulo pequeño este totalmente encajado en el grande. Diremos entonces que esos dos triángulos se encuentran en posición de Thales.

En una homotecia con centro el origen de coordenadas, se cumple que todo punto P(x,y) y su homólogo P´(x´,y´) se relacionan mediante las siguientes ecuaciones: x´=k*x, y´=k*y.

Esta unidad interactiva requiere la máquina virtual de Java J2RE.

Teorema fundamental de la Semejanza:

Dos triángulos en posición de Thales son semejantes.

Y, de manera recíproca: dos triángulos semejantes se pueden colocar en posición de Thales.

2.- ¿Son paralelos los lados BC y B´C´?
3.- ¿Qué diferencia hay entre los valores de la razón de semejanza de 0<1 y k<1?
4.- Relaciona la longitud de los lados BC y B´C´ para k=0.5.
5.- Comprueba la relación entre dos puntos B y B´ para k=2, k=0.5, k=-3, y k=-0.5.

	José Ignacio Nieto Acero

	Ministerio de Educación, Cultura y Deporte. Año 2011

Los contenidos de esta unidad didáctica están bajo una licencia de Creative Commons si no se indica lo contrario.