

TRANSFORMACIONES DE FUNCIONES I: TRASLACIONES
TRASLACIÓN VERTICAL
En la siguiente escena vas a poder observar como se modifica la gráfica de una función f(x) cuando se le suma una constante, es decir la gráfica de f(x)+a:
1.- La función que viene representa por la gráfica anterior es y=(x+3)*(x-4)*(x+2)/10. Cambia los valores del parámetro a y observa qué se modifica en la gráfica. (Para ello puedes usar los pulsadores o escribir directamente el valor del parámetro y pulsar intro)
2.- Describe qué relación guarda la gráfica de f(x) y la de f(x) + a.
3.- Indica qué características de las funciones se ven afectadas por estas traslaciones y cuáles quedan invariantes.
TRASLACIÓN HORIZONTAL
En la escena que viene a continuación se modifica la función sumándole también una constante, pero ahora esta operación se realiza sobre la variable independiente antes de aplicarle la función. La función que se obtiene es f(x+b):
1.- La función representada es la misma que en la situación anterior. Modifica los valores de b y observa cómo se traslada la gráfica.
2.- Describe las relaciones entre ambas gráficas
3.- ¿Cuáles son ahora los cambios en las características?
TRASLACIONES VERTICALES y HORIZONTALES
Ahora en esta actividad puedes modificar ambos parámetros en la función de partida o introducir tus propias funciones, la elemental (o inicial) a la izquierda y la transformada a la derecha.
1.- Indica los valores de a y b para que la función anterior:
a) Pase por el punto P(0,5)
b) Corte al eje de abscisas en un solo punto
c) Tenga un máximo en el origen de coordenadas
2.- Utiliza la escena anterior para estudiar traslaciones en los modelos exponencial y de proporcionalidad inversa.
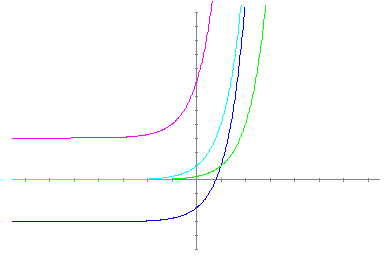
3.- En la siguiente imagen la gráfica celeste corresponde a y=4^x, obtén la expresión algebraica de las otras funciones.
Inicio Dilataciones Valor absoluto
|