Funciones elementales. La pendiente de la recta .
4º ESO DIVERSIFICACIÓN CURRICULAR
 
 
Rectas paralelas

Dos rectas son paralelas cuando tienen la misma pendiente.

ESCENA 6: Observa la siguiente escena:

- De color ROJO aparece una recta de ecuación y=mx, donde m (pendiente de la recta) vale 1 y se puede modificar con los pulsadores azul y rojo del control que aparece en la parte inferior de la escena.

- De color GRIS aparece otra recta de ecuación y=2x+3, cuya ecuación puedes modificar borrando y escribiendo sobre ella y pulsando la tecla INTRO.

  1. Utiliza los pulsadores de la parte inferior de la escena para modificar la pendiente de la recta roja hasta conseguir que sea paralela a la recta gris.

    a) Escribe las ecuaciones de las dos rectas. ¿Qué tienen en común?

    b) ¿Cuándo podemos decir que dos rectas son paralelas?

  2. Pulsa el botón inicio. Modifica la ecuación gris (escribiendo sobre ella y pulsando intro) hasta obtener 4 rectas paralelas a la roja, dos por encima de ella y dos por debajo, y anota sus ecuaciones.

  3. Pulsa el botón inicio. Modifica las dos funciones (gris y roja) hasta obtener dos rectas con igual pendiente y que pasen por el origen de coordenadas, pero una creciente y otra decreciente. Anota algunos ejemplos. ¿Cómo son entre sí las dos ecuaciones?

  4. ¿Cuándo queda una recta por encima de otra? ¿Y por debajo?

  5. Anota el punto de corte de cada recta con el eje y. ¿Qué relación tiene esta punto con la forma analítica de la función?
¿Cómo calcular la pendiente de una recta?

Es muy fácil: basta con trasladar la recta hasta hacerla pasar por el origen de coordenadas, elegir cualquier punto de ella y dividir el valor de la ordenada de ese punto por el de la abscisa.

"m = y/x"
ESCENA 7: Realiza las siguientes actividades y contesta las cuestiones propuestas.

  1. Traslada la recta roja, arrastrando el punto P, hasta hacerla pasar por el origen de coordenadas.

  2. Fíjate en un punto cualquiera de la recta y anota sus coordenadas. (Al hacer clic con el ratón te aparecerán las coordenadas pero procura usar esta ayuda sólo como herramienta de comprobación).

  3. Calcula la pendiente de la recta, dividiendo y entre x.

  4. En el control inferior (m), escribe la misma pendiente que has obtenido y comprueba cómo ambas rectas son paralelas.

  5. Elabora una tabla como la siguiente en tu ficha de trabajo (pulsa el botón inicio para generar una nueva recta):

Coordenadas de un punto cualquiera de la recta Pendiente Recta paralela
(2, 6)
6/2 = 3
y = 3x + 5
...
...
...

Pero para calcular la pendiente de una recta cualquiera basta con elegir dos puntos cualesquiera de esa recta y hallar el cociente entre la diferencia de los valores de las ordenadas y la diferencia de los valores de las abscisas de ambos puntos.

Es decir, dados dos puntos cualesquiera de una recta P(x1 , y1) y Q(x2 , y2 ), la pendiente sería:

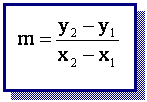
ESCENA 8: Elige dos puntos del plano P(x1, y1) y Q(x2, y2), e introduce las coordenadas "x1" y "x2"utilizando los pulsadores de la parte inferior de la escena. Completa después la siguiente tabla y calcula la pendiente de la recta:

  1. Escribe tres valores distintos para x1 y para x2 y comprueba, completando la siguiente tabla, que se obtiene el mismo valor de la pendiente. (Utiliza el zoom si el punto se te sale del plano).

    x1
    y1
    x2
    y2
    y2-y1
    		 x2-x1 m
    1
    3
    2
    0
    -3
    1
    -3
    ...
    ...
    ...
    ...
    ...
    ...
    ...

  1. Pulsa el botón inicio para obtener una nueva recta con una pendiente distinta. Vuelve a dar otros tres valores para x1 y x2.

  2. Repite el proceso con dos rectas más de manera que al final tengas dos ejemplos con rectas crecientes y otros dos con rectas decrecientes.
  Inmaculada Ordóñez Ríos
 
Ministerio de Educación, Cultura y Deporte. Año 2006
 
 

Licencia de Creative Commons
Los contenidos de esta unidad didáctica están bajo una licencia de Creative Commons si no se indica lo contrario.