|
|
|
| Análisis | |
|
|
|
| ÍNDICE | |
Una función f es continua continua en x=p si para valores de x que difieren poco de p, también los correspondientes f(x) difieren poco de f(p), es decir, si límite de f(x) cuando x tiende a p es f(p).
Una función f es derivable en x=p si existe f'(p) (que es el límite de (f(x)-f(p)) / (x-p) cuando x tiende a p).
La recta tangente a la gráfica de una función f en el punto de abscisa x=p tiene pendiente con valor f'(p).
Por tratarse de una función polinómica, la función parabólica es continua y derivable en todo su dominio (que es IR), es decir, para todo valor x real.
Ejercicio
3 |
Escena
3 |
a) Comprueba con la escena 3 dando diferentes valores a los coeficientes a, b y c que toda función parabólica es continua. b) Comprueba con la misma escena que toda función parabólica que consideres poseerá derivada f'(x) para cualquier x real que elijas. c) Halla en tu cuaderno f '(x), f '(-2),f '(0) y f '(2) para cada una de las siguientes funciones: f(x)=5x2+2x-1 f(x)=-3x2-2x+2 f(x)=-5x2 d) Observa en la escena 3 la recta tangente a la parábola en el punto de abscisa x=-2, x=0 y x=2 en cada uno de los casos del apartado c). |
MONOTONÍA
Recuerda que una función es monótona
creciente en un intervalo si ![]() para los x de dicho intervalo.
para los x de dicho intervalo.
De modo análogo se dice que una función es monótona
decreciente en un intervalo si ![]() para los x de dicho intervalo.
para los x de dicho intervalo.
Cuando las desigualdades se convierten en > o <, el crecimiento o decrecimiento es estricto.
Así que para cualquier función parabólica f(x)=ax2+bx+c, al ser f'(x)= 2ax+b, se tendrá que:
| f es estrictamente creciente en: | f es estrictamente decreciente en: |
| CASO a<0 |
| CASO a>0 |
EXTREMOS RELATIVOS
Se dice que un punto (p,f(p)) es un mínimo relativo de una función f (o que f alcanza mínimo relativo en x=p) si existe un entorno reducido de modo que para todo x de dicho entorno se cumple que f(p)<f(x) o f(p)=f(x)
Se dice que un punto (p,f(p)) es un máximo relativo de una función f si existe un entorno reducido de modo que para todo x de dicho entorno se cumple que f(p)>f(x) o f(p)=f(x)
EXTREMOS ABSOLUTOS
Se dice que un punto (p,f(p)) es un mínimo absoluto de una función f (o que f alcanza mínimo absoluto en x=p) si para todo x del dominio de f, se cumple que f(p)<f(x) o f(p)=f(x)
Se dice que un punto (p,f(p)) es un máximo absoluto de una función f si para todo x del dominio de f, se cumple que f(p)>f(x) o f(p)=f(x)
CÁLCULO DE EXTREMOS
En la práctica, para calcular los extremos de una función f se utiliza el siguiente resultado:
Si f'(p)=0 y f''(p)<0 , f tiene un máximo en x=p
Si f'(p)=0 y f''(p)>0 , f tiene un mínimo en x=p
por lo que para f función parábolica, como f'(-b/(2a))=0 y f''(-b/(2a))=2a (de hecho f''(x)=2a) se tendrá que:
todas funciones parabólicas con a>0 poseen un mínimo absoluto en x=-b/2a, es decir:
el punto 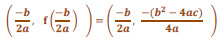
es el mínimo absoluto de f en el caso a>0, y es el máximo absoluto de f en el caso a<0. Dicho punto es al que llamamos vértice de la parábola.
Y la ordenada de dicho punto y el hecho de fijarnos en si la parábola se abre hacia arriba (a>0) o hacia abajo (a<0) nos permiten deducir el recorrido de f que ya se expuso en el punto 2 de esta Unidad Didáctica.
Ejercicio
4 |
Escena
4 |
a) Halla en tu cuaderno las zonas de crecimiento y de decrecimiento de las siguientes funciones: f(x)=2x2-10x+12 f(x)=-x2-1 f(x)=-2x2+4x-4 Usando la escena 4 comprueba tus resultados. b) Calcula los extremos de las funciones del apartado anterior usando el resultado del punto 5 de esta Unidad para calcular extremos, anotando todo en tu cuaderno y comprobando después en la escena las soluciones. |