|
DE LA FUNCIÓN EXPONENCIAL A LA
FUNCIÓN LOGÍSTICA |
| Análisis | |
| 2.
LA FUNCIÓN EXPONENCIAL |
||
| En
primer lugar vamos a plantearnos un problema con un crecimiento
exponencial y después veremos cómo se puede transformar en una
situación de crecimiento logístico. |
||
|
|
Se ha observado que el número de personas afectadas por una enfermedad contagiosa aumenta diariamente a un ritmo del 60%. Inicialmente se han detectado 10 personas enfermas.
1.- Escribe la expresión analítica de la función que nos da el número de personas afectadas, N(t), dependiendo del número de días transcurridos t. 2.-
Queremos expresar la función anterior como una exponencial de base e, del tipo  |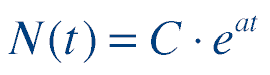
|
|
||
|
||
| 3.
LA FUNCIÓN LOGÍSTICA |
||
| Supongamos
ahora que estamos estudiando la evolución de la enfermedad en un
instituto que tiene mil alumnos, por tanto el contagio sólo puede
extenderse, como máximo a 1000 personas. Según hemos dicho, inicialmente la función logística se comporta como una exponencial y el parámetro a es el mismo en las dos funciones, es decir, las ecuaciones de una población P(t) exponencial y logística son  |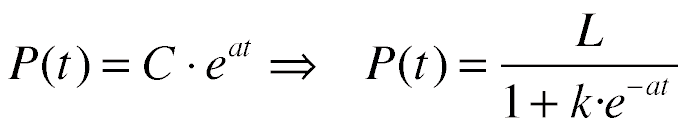
||
|
|
En
nuestro caso sabemos, que si el crecimiento fuese ilimitado el número
de infectados es 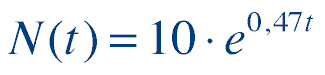 1.- En la función logística, ¿qué valores toma el parámetro a? ¿Y el parámetro L? Sustitúyelos en la ecuación. 2.- Teniendo en cuenta que en el instante inicial hay 10 enfermos y que ambas funciones coinciden, halla el valor del parámetro k. Ahora
ya tienes la ecuación de la función logística.
|
|
|
||
 |
 |
 |
||||
 |
| Ana
Pola
Gracia |
||
 |
||
| Ministerio de Educación, Cultura y Deporte. Año 2010 | ||
Los
contenidos de esta unidad didáctica están bajo una licencia
de Creative Commons si no se indica lo contrario.
, si queremos transformarla en 
sólo tenemos que despejar 
, por tanto, 
,
para valores próximos a cero.