
 |
ESTUDIO DE FUNCIONES ELEMENTALES |
|
Para dibujar una función definida a trozos podemos actuar de dos formas
distintas: a) Podemos dibujar cada una en todo el plano y una vez dibujadas todas, borramos del plano la parte de la gráfica que no entre en el intervalo para el que estaba definida b) Señalamos en el eje de abscisas los intervalos y vamos dibujando en cada uno la gráfica que a él corresponda este método es el utilizado en la escena anterior). En ambos casos, pero en este último más es muy interesante conocer cuánto vale la función en cada uno de sus extremos. Así afinaremos bastante la gráfica. |
.Actividad 21.- Dibuja en tu cuaderno de trabajo las gráficas de las siguientes funciones definidas a trozos. Comprueba después tus ejercicios resueltos usando la escena de más abajo:
Ejercicio nº 1: Ejercicio nº 2: Ejercicio nº 3: Ejercicio nº 4:
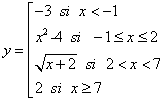
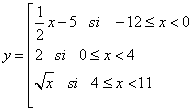
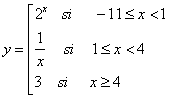
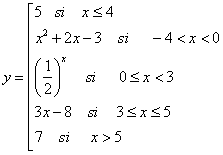
|
|
|
 |
José Manuel Uceda Ortega | |
| Ministerio de Educación, Cultura y Deporte. Año 2007 | ||

Los contenidos de esta unidad didáctica están bajo una licencia de Creative Commons si no se indica lo contrario.