3. LA DIFERENCIAL DE UNA FUNCIÓN f

Análisis.

Bachillerato de la modalidad de Ciencias de la Naturaleza y de la Salud o Tecnológico

3.1  DIFERENCIAL DE UNA FUNCIÓN
En el estudio de la derivada de una función se llega a la expresión de la derivada de la función f en un punto x:

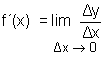o lo que es lo mismo, a que

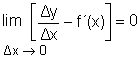por lo que podemos afirmar que

 

               es un  infinitésimo ( ε →  0 ) cuando 

Multiplicando entonces los dos miembros de esa igualdad por Δx  y despejando a continuación Δy  se obtiene la siguiente expresión para Δy:

   Δy  =  f ´(x) . Δx +  ε . Δx ,  con ε →  0  cuando  Δx →  0

Aparece entonces Δy expresado como suma de dos sumandos:

 por un lado,             f ´(x) . Δx 

 y por otro,                    ε . Δx  

Los dos son obviamente infinitésimos cuando Δx →  0, y en consecuencia  Δy también.

Ahora bien, en los puntos x en los cuales f ´(x) ≠  0, se tiene

 

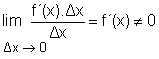
por lo que f ´(x) . Δx e Δx son infinitésimos del mismo orden, mientras que

 

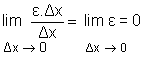por lo que  ε . Δx es un infinitésimo de orden superior a Δx.

Comprueba:

En la escena de arriba, puedes variar el punto x con el pulsador correspondiente, y el Δx con su pulsador, o directamente con el puntero del ratón sobre el control gráfico.

Deja el punto x fijo allí donde quieras y haz que el Δx tienda a cero. Comprueba entonces lo que se ha dicho más arriba relativo a Δy, Δx, f ´(x).Δx  y  ε.Δx. Observa también arriba a la izquierda los valores que van tomando cada uno de ellos.

Tarea 3:

Haz una tabla en la que en cada columna figure el valor que toman   Δx, Δy, f ´(x).Δx  y  ε.Δx, al ir variando Δx desde el valor inicial 2 hasta 0,01, pasando por los valores intermedios 1, 0´5, 0'1, 0´05 y 0´03, 0´01. Confirma con los resultados obtenidos lo que has observado anteriormente.

Comprueba:

La escena de la derecha proporciona la gráfica descrita por la variación de esos cuatro infinitésimos en la situación de la escena anterior, a medida que Δx →  0.

Actívala y aplica lo estudiado en el apartado de infinitésimos para comprobar que dichos infinitésimos cumplen lo afirmado más arriba

A la vista de la gráfica, ¿qué tipo de relación crees que existe entre  Δy  y   f ´(x).Δx ?

Así pues, cuando Δx →  0, Δy queda expresado como suma de dos sumandos, uno de los cuales es un infinitésimo del mismo orden que Δx y el otro un infinitésimo de orden superior a Δx, es decir, que converge hacia 0 mucho más rápidamente que Δx, por lo que puede considerarse despreciable, frente al otro sumando, que es la parte principal del infinitésimo Δy.

Se da entonces la siguiente definición:

   Si la función f es derivable en el punto x, se llama diferencial de la función f  y se representa por dy a la parte principal del infinitésimo Δy:

dy  =  f ´(x) . Δx

Es decir, para los valores de x en los que f ´(x) ≠  0, y si Δx →  0,  dy es la parte principal del infinitésimo Δy, es del mismo orden que el infinitésimo Δx y es una función lineal de Δx, en la que la constante de proporcionalidad es f ´(x).

  • Si aplicamos dicha definición a la función  y = x, tendremos:

 

Por un lado, obviamente  dy  =  dx

Según la definición,         dy  =  f ´(x) . Δx  = x´. Δx  = 1 . Δx  = Δx

En consecuencia,  dx  =  Δx, es decir, la diferencial de la variable independiente coincide con el incremento de dicha variable.

Si llevamos este resultado a la definición de la diferencial, tendremos que, en general,

dy  =  f ´(x) . dx , que nos proporciona la conocida notación de Leibnitz para la derivada:

Con lo dicho anteriormente es fácil demostrar el siguiente importante teorema:

Una función f(x) es diferenciable en un punto si y solo si es derivable en dicho punto

que hace que en muchas ocasiones se utilicen los términos diferencial, diferenciable,... en lugar de derivada, derivable,...

3.2  INTERPRETACIÓN GEOMÉTRICA

 

 

Geométricamente, la diferencial representa el incremento de la variable dependiente, pero no hasta la curva, sino hasta la tangente:

Δy = SQ = ST + TQ , por lo que   dy = ST

Tarea 4:

Aplica la expresión  dy=f ´(x).dx  para hallar la diferencial de las funciones que siguen, en el punto  x  y para el valor dx  que se indica en cada caso, y a continuación halla Δy. Compara ambos valores:

y = f(x) =7x3                    x = 2                 dx = 0,001

y = g(x) = x.sen x             x = π/4              dx = 0,001

y = h(x) = 1+L x               x = 3                  dx = 0,01

Lo visto en esta última tarea y en la comprobación de la escena anterior nos proporciona una pista para responder a la pregunta que se hacía en dicha comprobación: ¿qué tipo de relación existe entre  Δy  y   dy = f ´(x).Δx ?

 

Se tiene

 

,por lo que podemos enunciar el siguiente teorema:

Teorema.- Si f´(a) ≠ 0, entonces dy e Δy son infinitésimos equivalentes en x=a, cuando Δx →  0

En consecuencia, se podrá sustituir uno por otro en las condiciones indicadas por el teorema de sustitución de infinitésimos equivalentes enunciado anteriormente.

De hecho, en la práctica suele utilizarse la diferencial como un valor aproximado del incremento de la función.

Comprueba:

Utiliza el botón  para comprobar los resultados obtenidos en la tarea 4. 

 

 

  Cándido Teresa Heredia
 
Ministerio de Educación, Cultura y Deporte. Año 2004
 
 

Licencia de Creative Commons
Los contenidos de esta unidad didáctica están bajo una licencia de Creative Commons si no se indica lo contrario.