
Análisis.
Bachillerato de la modalidad de Ciencias de la Naturaleza y de la Salud o Tecnológico
 |
4. APLICACIONES DE LA DIFERENCIAL |
|
Análisis. Bachillerato de la modalidad de Ciencias de la Naturaleza y de la Salud o Tecnológico |
|
|
|
| 4.1 ALGUNAS APLICACIONES DE LA DIFERENCIAL | |
|
Entre las aplicaciones prácticas del concepto de diferencial de una función vamos a tratar aquí los relacionados con la utilización de dos resultados obtenidos en las líneas anteriores: |
|
|
|
|
|
|
CASO 1º En la expresión Δy = f ´(x).Δx + ε .Δx, podemos escribir Δy = f(x+Δx) - f(x) y prescindir del sumando ε .Δx, con lo que nos queda, para un valor fijo x = a, Δy = f(a+Δx) - f(a) ≈ f ´(a).Δx, de donde f(a+Δx) ≈ f(a) + f ´(a).Δx = f(a) + dy , igualdad que es útil para obtener valores aproximados de f para valores próximos a x=a, utilizando para ello f(a) y df(a) con un determinado Δx. |
|
Gráficamente, lo que estamos haciendo es sustituir la ordenada de la imagen de a+Δx sobre la gráfica de la función por la ordenada de su imagen sobre la gráfica de la tangente, despreciando el infinitésimo ε .Δx. |
|
Ejemplo 1. Hallar un valor aproximado de sen 33º . Se trata de aplicar la expresión anterior a la función f(x) = sen x, con a = 30º ( π/6 rad) e Δx = 3º ( 3π/180 rad). Es decir, sen 33º = sen (30º + 3º) = sen ( π/6 + 3π/180 ) ≈ sen π/6 + (sen π/6)´ . (3π/180) = sen π/6 + cos π/6 . (3π/180) =
|
|
|
|
|
|
Ejemplo 2. Hallar un valor aproximado de cotg 58º . Se trata de aplicar la expresión anterior a la función f(x) = cotg x, con a = 60º ( π/3 rad) e Δx = -2º ( -2π/180 rad), es decir, para un Δx negativo. Tendremos, cotg 58º = cotg [60º + (-2º)] = cotg [ π/3 + (-2π/180 )] ≈ cotg π/3 - 1/(sen2 π/6) . (-2π/180) =
|
|
|
|
Ejemplo 3. Hallar
un valor aproximado de
Consideremos la función f(x) = x1/3, el valor a = 0,125 = 1/8 y el Δx = 0,02: |
||
|
|
= f (0,125 + 0,02) = f(1/8) + f ´(1/8) . 0,02 = |
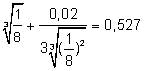
|
|
|
|
Ejemplo 4. Hallar un valor aproximado de 0,822 Consideremos la función f(x) = x2, el valor a = 0,8 y el Δx = 0,02: 0,822 = f(0,8 + 0,02) = f(0,8) + f´(0,8) . 0,02 = = 0,64 + 2.0,8.0,02 = 0,672 |
|
|
|
Tarea 5: Halla un valor aproximado de a) cos 47º b) e3,05 c) 1,023 |
|
CASO 2º Anteriormente se ha enunciado el teorema que dice que dy e Δy son infinitésimos equivalentes en x=a cuando Δx → 0, si f´(a) ≠ 0 por lo que, aplicando el teorema de sustitución de infinitésimos equivalentes, podremos sustituir Δy por dy en las condiciones adecuadas, con el objeto de simplificar el problema. |
|
Ejemplo 5. Un depósito tiene forma de esfera de 3 m de radio. Estimar cuánto aumentará el volumen del depósito si el radio aumenta 5 cm. El
volumen de la esfera viene dado por Se trata de hallar ΔV para Δr = 5 cm, para lo cual hallaremos ΔV ≈ dV = V´(r) . dr = 4π.r2 . dr = 4π.9.0,05 = 5,655 m3
|
|
Ejemplo 6. Se sabe que en determinadas placas cuadradas para circuitos impresos, con el aumento de temperatura en el funcionamiento del procesador se produce una dilatación lineal de los lados de las placas del 0,4 %. El lado de cada placa mide 7 mm. Calcular aproximadamente el aumento en el área de la placa. El área de la placa es A = l2. Por tanto hemos de hallar ΔA para Δl = 0,028 mm (0,4 % de 7 mm) para lo que calcularemos dA: ΔA ≈ dA = A´(l) . dl = 2.l.dl = 2.7.0,028 = 0,392 mm2. Es decir, el área aumenta aproximadamente un 0,8 %.
|
|
Ejemplo 7. Un instrumento de medida que aproxima sólo hasta los milímetros proporciona para el radio de un círculo una longitud de 14 m. Estimar el error absoluto máximo esperable en el cálculo del área del círculo. El área del círculo A = π.r2. Por tanto hemos de hallar ΔA para Δr = 0,001 mm, para lo que calcularemos dA: Error absoluto máximo esperable = ΔA ≈ dA = A´(r) . dr = 2.π.r.dr = 2.π.14.0,001 = 0,08796 m2.
|
|
Tarea 6: Enuncia un problema del tipo de cada uno de los tres vistos y resuélvelo a continuación. |
| Cándido Teresa Heredia | ||
 |
||
| Ministerio de Educación, Cultura y Deporte. Año 2004 | ||

Los contenidos de esta unidad didáctica están bajo una licencia de Creative Commons si no se indica lo contrario.