

Polígonos regulares y el teorema de Pitágoras
Un polígono es un figura plana cerrada, formada por segmentos. Cada segmento se le llama lado.
Un polígono regular es un polígono con todos los lados y ángulos iguales.
Un polígono regular de n lados siempre se puede descomponer en n triángulos isósceles. ¿Por qué?
Cuantos más lados tenga el polígono regular, más se ajusta a la circunferencia. ¿Por qué?
Cada triángulo isósceles se divide con la altura en dos triángulos rectángulos. A la altura se le llama apotema.
En ese triángulo rectángulo se puede aplicar el teorema de Pitágoras para relacionar el lado, el radio de la circunferencia circunscrita y la apotema.
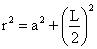
|
A. Esta escena es descriptiva y tienes la posibilidad de cambiar el número de lados y de seleccionar diferentes aspectos. |
|
B. Prueba a cambiar para que te vayas familiarizando con la escena. |
|
C. En selección 1, puedes ver como se forman los triángulos isósceles. |
|
D. En selección 2, calcula la apotema, el lado y el perímetro. |
|
E. En selección 3, calcula áreas. Para ello hay que recordar como se calcula el área de un triángulo y la relación entre el polígono y los triángulos que se forman. |
Actividades
Cuantos más lados tiene el polígono regular, ¿el lado es mayor o menor?
¿Cuándo el lado coincide con el radio de la circunferencia circunscrita?
Si el número de lados aumenta en una circunferencia de radio 1, ¿el perímetro y el área a qué números se aproximan?
Realiza en tu cuaderno los cálculos y comprueba en la escena los siguientes ejercicios:
Calcula la apotema de un hexágono de radio 5 cm y su perímetro.
En un cuadrado, la apotema vale 3 cm y el lado 6. Calcula el radio de la circunferencia circunscrita y el perímetro del cuadrado.
En un pentágono, el radio vale 4 cm y la apotema 3.24 cm. Calcula el lado y el perímetro del pentágono.
Calcula el área de las figuras anteriores.
|
|||||||||||||||