

Circunferencia y el teorema de Pitágoras
Los elementos de una circunferencia son la cuerda, el radio, el arco y la flecha.
Las posiciones relativas de una recta y una circunferencia pueden ser: Secantes, tangentes o no se cortan.
Siempre en una circunferencia, una cuerda forma un triángulo isósceles con los radios que acaban en los extremos de la misma. Con la altura sobre la cuerda siempre tenemos un triángulo rectángulo.
En ese triángulo rectángulo se verifica:
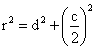
|
A. En selección 1, puedes ver los elementos de una circunferencia. |
|
B. En selección 2, vas a calcular las longitudes de los elementos anteriores. |
|
C. En selección 3, vas a calcular áreas y perímetros de sectores circulares. |
|
D. En selección 4, vas a calcular áreas de sectores circulares. |
|
E. En selección 5, puedes ver las posiciones de una circunferencia y una recta. |
|
F. Los puntos gruesos y rojos los puedes mover con el ratón. |
Actividades
Haz los cálculos en el cuaderno y comprueba los resultados en la escena, utilizando las herramientas oportunas.
Si la corona circular es lo que queda dentro de dos circunferencias concéntricas, ¿cómo calculas su área?
Si en una circunferencia, una cuerda mide 7.2 cm y su distancia al centro es 1.74 cm. ¿Cuánto mide el radio de la circunferencia?
Si el el radio de una circunferencia es 3 cm., ¿cuál es la longitud de una cuerda que está a 1.5 cm del centro?
Si tienes una circunferencia de radio 5, ¿cuál es la longitud de la cuerda más grande posible?
Fijado un punto, ¿cuántas cuerdas hay que midan 5 cm, si la circunferencia es de radio 4 cm? Calcula la distancia de esa cuerda al centro de la circunferencia.
Si en una circunferencia de 12 cm de radio, se traza una cuerda AB a 12 cm del centro, ¿cuánto mide la cuerda?
Desde un punto D que dista 8 cm del centro de una circunferencia de radio 4, se traza una tangente. Calcula la distancia de D al punto de tangencia.
Si trazamos una tangente desde un punto D a una circunferencia, la distancia entre ese punto y el de tangencia es 9 cm, si el radio es 6 cm, ¿Qué distancia hay de D al centro de la circunferencia?
|
|||||||||||||||