 |
LA HIPÉRBOLA
|
| 4.-
Relación entre a,b,c: c2
= a2 + b2 |
Observa
la escena y fijate que a,b,c son las medidas de los
lados de un triángulo rectángulo.En
esta escena vamos a comprobar que la relación c2
= a2 + b2
se cumple en cualquier hipérbola.Recuerda que 2a
es la medida del eje real , 2b
es la medida del eje imaginario y 2c
es la distancia focal.
|
|
- Comprueba para distintos
valores de a y c que
se cumple la relación.
|
- Calcula en tu
cuaderno el valor que falta, luego comprueba en
la escena que lo has hecho bien
| a |
b |
c |
| 8 |
6 |
? |
| ? |
12 |
13 |
| 9 |
? |
15 |
|
- ¿Puede se c=0?
|
| |
|
|
Habrás
observado en las distintas escenas que unas hipérbolas tienen
las ramas más abiertas que otras. Esta característica de
ser más abierta o más cerrada se mide con un número e
llamado excentricidad.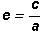 
con c >
a luego será e>1.
Por tanto fijado
el valor de a , se tiene que cuánto más próxima
esta la excentricidad a 1 más cerradas son las
ramas de la hipérbola . Por el contrario cúanto mayor es
la excentricidad más abiertas son las ramas de la hipérbola.
|
|
- Mueve el control
excentricidad y observa como cambia el aspecto de
la hipérbola en función de su valor.
- ¿Cómo es el dibujo de la
hipérbola si e=1?
- ¿A que se acerca el
dibujo de la hipérbola si la excentricidad se
hace grande?
|
| Las
asíntotas de la hipérbola son dos rectas
a las que la curva se acerca idefinidamente sin llegar a
tocarla. |
| Para
trazar las asíntotas de la hipérbola se traza primero
el rectángulo de lados paralelos a los ejes y que tienen
por dimensiones 2a y 2b y su
centro coincide con el de la hiperbola. Luego se trazan
las diagonales del rectángulo que son las
asíntotas de la hipérbola. En esta
escena vamos a comprobar que la asíntota se acerca a la
gráfica tanto como queramos para valores grandes de x,
es decir para un valor de x el valor de
y en la recta va a ser casi igual que el
valor de y en la hipérbola
Para verlo utiliza el zoom y mueve los ejes. En la escena
se ven y los dos valores de y y
su diferencia.
|
|
|
- Mueve el control (Punto verde) y observa cual es
el valor de la y en la recta y en la hipérbola.
Fijate que su diferencia se acerca a cero
conforme alejamos el control
|
| |
- Dibuja en tu cuaderno las asíntotas y la hipérbola
de parámetros a=3 b=5
|
| |
Miguel
Ángel Cabezón Ochoa |
 |
Ministerio de Educación, Cultura y Deporte. Año 2003 |
| |
|
Los contenidos de esta unidad didáctica están bajo una licencia de Creative Commons si no se indica lo contrario.
