indice cónicas 4º ESO B


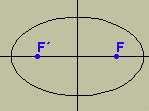
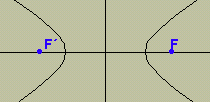
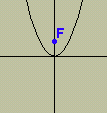
LA ELIPSE LA HIPÉRBOLA LA PARÁBOLA DIBUJO POR PUNTOS		Una superficie cónica de revolución es una superficie engendrada por una recta g (generatriz) que gira alrededor de otra recta e (eje), con la cuál se corta en un punto V (vértice). Si a una superficie cónica la cortamos por un plano que no pasa por el vértice, la intersección que resulta es una curva que recibe el nombre de cónica. Apolonio de Pérgamo, geómetra griego del siglo III antes de J.C. es el autor del más importante tratado antiguo dedicado a estas curvas *Las Cónicas,* en ella demuestra como se pueden obtener las tres curvas cortando un cono con un plano orientado de distintos modos. No se les descubrió ninguna aplicación científica importante hasta el siglo XVII, cuando Kepler descubrió que los planetas se mueven en órbitas elípticas y Galileo demostro que las trayectorias de los proyectiles son parabólicas.

		OBJETIVOS Dibujo de las cónicas. Definir las cónicas: elipse, hipérbola y parábola. Describir los elementos de la elipse, hipérbola y parábola. Focos Radio Vectores Ejes Vértices Centro Relación entre a,b,c en la elipse y la hipérbola. Definir la excentricidad de la elipse, hipérbola. Trazar la elipse, hipérbola y parábola. Asíntotas de una hipérbola. Conocer la superficie de una elipse. Construcción por puntos de las cónicas.

Los contenidos de esta unidad didáctica están bajo una licencia de Creative Commons si no se indica lo contrario.

	*Miguel Ángel Cabezón Ochoa*
	Ministerio de Educación, Cultura y Deporte. Año 2003

LAS CÓNICAS 4º Eso B