|
Pitágoras de Samos (580-500 aC): Es
un personaje aún más misterioso que Thales. Vivió unos 50 años después
de éste y, en su juventud, viajó por Egipto, Babilonia y posiblemente
la India, países en los que adquirió su formación matemática y filosófica.
Contemporáneo de Buda, Confucio y Lao Tse, estuvo muy influido por el
misticismo religioso. Se dice que era vegetariano ya que creía en la
trasmigración de las almas. Se estableció en Crotona, al sudeste de
Italia, entonces parte de Grecia, donde fundó una secta secreta, los
pitagóricos, que contribuyeron en el mundo heleno a la difusión y
desarrollo de las matemáticas. La primera referencia escrita vuelve
a aparecer en la obra de Proclo (410-485dC) "Comentario sobre el primer
libro de los Elementos de Euclides". Inmediatamente después de escribir
sobre Thales, Proclo escribe: "transformó esta ciencia en una
forma de educación liberal, examinando sus principios desde el comienzo y
demostrando los teoremas de una manera inmaterial e intelectual. Así
descubrió la teoría de las proporciones y la construcción de las
figuras cósmicas". Fueron los pitagóricos los primeros que se
dedicaron al estudio, movidos por el amor a la sabiduría y la belleza y no
por cuestiones de tipo práctico. Parece que es difícil separar la
historia y la leyenda en lo que se refiere a Pitágoras, pero sí está
clara la influencia de su escuela en el desarrollo de la matemática
griega. Veamos algunos aspectos relevantes: |
Utilizaban para la
obtención de ternas pitagóricas las
expresiones 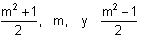 pero éstas ya eran conocidas por los
babilónicos. pero éstas ya eran conocidas por los
babilónicos.
Se
les atribuye la demostración
del teorema de Pitágoras,
conocido también por los babilónicos, pero no existe una
prueba clara de esto. Aquí vas a ver una demostración que utiliza la semejanza de
triángulos y la proporcionalidad de segmentos. |
|
|
| La
altura es media proporcional entre los dos segmentos en que divide a la
hipotenusa |
1.- Al trazar la altura en la figura se han
formado dos triángulos rectángulos semejantes. Los llamaremos mbh
y nhc.
Observa que tienen los ángulos iguales y, por
tanto, sus lados correspondientes son proporcionales.
| Si
quieres manipular la escena pulsa sobre ella el
botón derecho del ratón y aparecerá un
menú que te permite hacer un zoom
y centrar la imagen |
|