|
|
En
esta escena tienes 6 ejemplos de funciones definidas a trozos.
En
la primera de ellas se observas claramente tres trozos de rectas. Los
extremos de cada uno de estos trozos se resaltan con los símbolos que
hemos aprendido en las anteriores escenas. Los tres trozos se
corresponden con
x<-1 , -1<=x<1
y 1<=x.
Observa que para x=1
o x=-1,
sólo uno de los extremos puede estar cerrado porque si no la función
tendría dos valores para x=1
o x=-1 y
por tanto no sería función.
En
el segundo ejemplo también observamos tres trozos de rectas, pero esta
vez los extremos coinciden y "empalman" correctamente, se junta un
punto relleno con uno vacío, y, por tanto, ya no hace falta resaltar
los extremos.
Observa
el resto de ejemplos para ir
familiarizándote con este tipo de funciones.
|
Ejercicio
5:
Fíjate en las siguientes expresiones, es la expresión analítica de las
funciones definidas a trozos que presentamos como ejemplos en la escena
anterior. Relaciona cada una de estas expresiones con las gráficas de
la escena:
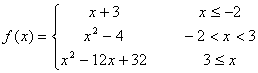
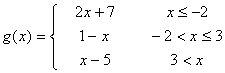
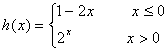
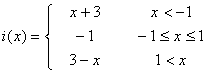
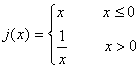
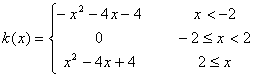
Ejercicio 6:
Para cada una de las gráficas anteriores calcula: Dominio, recorrido,
intervalos de crecimiento y decrecimiento, máximos y mínimos e
inyectividad.
Ejercicio 7:
Calcula f(-2), f(3), f(0), g(-2), g(-4), g(5), h(0), h(1/2),
i(1), i(0), j(0), j(1), j(-1), k(-1), k(2).
|
|
Esta
escena es una "máquina" para dibujar funciones definidas a trzos.
Puedes dibujar una función de hasta 3 trozos definiendo llos intervalos
con los parámetros inferiores y escribiendo la fórmula de la función en
las casillas que estan encima de ellos.
Familiarízate
con la escenba dibujando alguna de las funciones a trzos de la escena
anterior.
|
Ejercicio 8: Dibuja
las gráficas de las siguientes funciones a trozos. Además de ayudarte
de la escena anterior construye tablas de valores para cada uno de los
trozos.
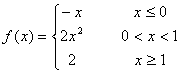
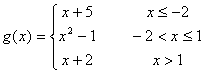
|
|


