TIPOS Y OPERACIONES
En esta Unidad Didáctica se buscan las relaciones entre las expresiones algebraicas de las funciones y sus representaciones gráficas. Para lo cual, se presentan las principales familias de funciones: rectas, parábolas, potencias y raíces n-ésimas de x, hipérbolas y trigonométricas. Se nos permite modificar ciertos parámetros y así "vemos" los cambios que se producen en la representación gráfica y deducimos su significado.
Así mismo, se estudian las operaciones básicas con funciones (suma, resta, multiplicación, división y composición) destacando también su significado gráfico.
Si se siguen atentamente las indicaciones y se resuelven los ejercicios propuestos, al final podremos esbozar la gráfica de una función (sencilla) conociendo la fórmula algebraica de dicha función.
- Identificar rectas con expresiones de la forma y=mx+n
- Comprender el concepto de pendiente de una recta y asociarlo al valor de m
- Comprender el concepto de ordenada en el origen de una recta y asociarlo al valor de n
- Estudiar los cambios que se producen en la recta y=mx+n al variar los valores de m y n.
- Identificar parábolas de eje vertical con expresiones de la forma y=ax2+bx+c
- Estudiar los cambios que se producen en la parábola y=ax2+bx+c al variar los valores de a, b y c.
-
Identificar parábolas de eje horizontal con expresiones de la forma
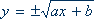
-
Estudiar los cambios que se producen en la parábola
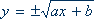 al variar los valores de a y b.
al variar los valores de a y b.
- Reconocer la forma que tiene la función y=xn para valores naturales de n
-
Reconocer la forma que tiene la función
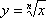 para valores naturales de n
para valores naturales de n
- Identificar hipérbolas equiláteras con expresiones de la forma y=k/x
- Estudiar los cambios que se producen en la hipérbola y=k/x+a al variar los valores de k y a, especialmente si k es positivo o negativo.
- Reconocer la forma que tienen las funciones trigonométricas seno, coseno, tangente, cosecante, secante y cotangente
- Comprender el concepto de período de una función y su significado gráfico.
- Hallar el período de una función trigonométrica sencilla.
- Estudiar los cambios que se producen en las funciones
y=sen(kx),
y=cos(kx),
y=tan(kx),
y=csc(kx),
y=sec(kx),
y=cot(kx)
al variar los valores de k.
- Entender el significado gráfico de la suma, resta, producto, división y composición de funciones.
- Entender el significado gráfico de la suma de una función más una constante.
- Entender el significado gráfico de la función inversa de una función.
- Conocer un método analítico para hallar la función inversa de una función.