|
|
|
Sea A un punto interior de una circunferencia de centro O. Hallar el lugar geométrico de los centros de las circunferencias que pasan por el punto A y son tangentes a la circunferencia dada.
Observación: Teniendo en cuenta el procedimiento geométrico para trazar una circunferencia que pase por dos puntos y sea tangente en uno de ellos a una circunferencia, el problema anterior puede enunciarse de la siguiente manera:
Sea B un punto de una circunferencia y A un punto interior a ella. Sea P el punto de intersección de la mediatriz del segmento AB con el radio OB. Hallar el lugar geométrico que describe el punto P cuando B recorre la circunferencia.
|
En este applet cuando el control B recorre la circunferencia el punto P describe una elipse. |
|
Para poder obtener la ecuación del lugar geométrico pedido debemos resolver previamente las dos observaciones siguientes:
|
Como el punto P pertenece a la mediatriz del segmento AB, ¿qué relación existe entre las longitudes de los segmentos AP y BP? |
|
Determinar la suma de las longitudes de los segmentos OP y AP. |
Atendiendo a las recomendaciones anteriores, para obtener la ecuación del lugar geométrico pedido en el problema anterior debemos realizar los pasos que se indican a continuación:
|
Situar un sistema de coordenadas con origen el centro de la circunferencia y eje en la dirección del segmento OA. |
|
Determinar la longitud del semieje mayor y la semidistancia focal. |
|
Determinar la ecuación del lugar geométrico |
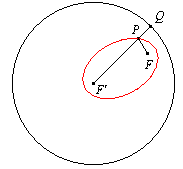Este problema se basa en el concepto de circunferencia focal de una elipse. Para
cada punto P de la elipse tomemos sobre la semirrecta que contiene al radio vector PF¢ un punto Q tal que la longitud del segmento PQ
sea igual a la del radio vector PF. Puesto que la suma de las longitudes PF
+ PF¢ es constante e igual a 2a, PF¢ + PQ = PF¢ + PF = 2a, el lugar geométrico de los
puntos Q obtenidos al variar el punto P sobre la elipse es una
circunferencia de radio 2a y centro F¢,
que se llama circunferencia focal. Existe una para cada foco. El segmento PQ = PF
es la distancia del punto P a la circunferencia focal. Como consecuencia de esto
podemos dar como definición de elipse la siguiente.
Definición: Una elipse es el lugar geométrico de los puntos del plano equidistantes de una circunferencia y de un punto interior.
Observando que la circunferencia de centro P y radio PF es tangente a la circunferencia focal F resulta también:
Definición: Una elipse es el lugar geométrico de los centros de la circunferencia tangentes a una fija y que pasan por un punto interior.
Una primera pregunta que debemos hacernos es ¿qué ocurrirá si el punto F es exterior a la circunferencia?. La respuesta la encontramos en el siguiente applet.
|
Mover el control A situándolo dentro o fuera de la circunferencia. |
|
Pulsar el botón limpiar para eliminar el rastro dejado por el punto P. |
|
Cuando el control B se mueve sobre la circunferencia el punto P describe una cónica. |
 |
 |
 |
Autor: Antonio Berhó Rodríguez
 |
Alumno |
| Ministerio de Educación, Cultura y Deporte. Año 2001 | |
| Alumno |
