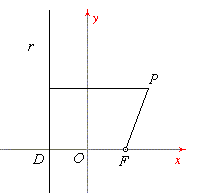
|
|
|
Para
determinar la ecuación canónica o reducida de una parábola situemos un sistema de
referencia de manera que el eje de abscisas coincida con el eje de la parábola y el
origen O, con el punto medio del segmento DF, donde D es la
proyección ortogonal del foco F sobre la directriz. Pongamos PF = p,
entonces el punto F en este sistema de referencia tiene por coordenadas F (
p/2, 0) y la ecuación de la directriz es r º
x + p/2 = 0. Sea P (x, y) un punto cualquiera del plano,
por definición de parábola la igualdad
|
[1] |
es una condición necesaria y suficiente para que el punto P pertenezca a la parábola. Como
|
|
[2] |
la relación
|
[3] |
es, en virtud de [1] la condición necesaria y suficiente para que el punto P (x, y) esté en la parábola. Elevando al cuadrado los dos miembros y simplificando los términos semejantes podemos escribir esta fórmula en la forma
|
[4] |
Debemos asegurarnos que la ecuación [4] deducida de [3] por transformaciones algebraicas no contiene raíces extrañas. Es suficiente con mostrar que la relación [1] se verifica para todo punto P (x, y) cuyas coordenadas x e y satisfagan la ecuación [4].
De la relación [4] se sigue que las abscisas x de los puntos considerados son mayores o iguales que cero. Para estos puntos se tiene que d (P, r) = x + p/2. Encontremos la expresión del radio vector PF del punto P. Sustituyendo el valor de y² de [4] en la igualdad [2] y, teniendo en cuenta que x = 0, se encuentra que PF = x + p/2. Así pues, PF = d (P, r) para estos puntos; es decir que estos puntos están sobre la parábola. La ecuación [4] se denomina ecuación canónica de la parábola.
Vamos a determinar ahora la ecuación de una parábola cuando la mediatriz del segmento DF y el eje de la parábola son paralelos a los ejes de coordenadas. Si las coordenadas del origen de los nuevos ejes de coordenadas es O¢(h, k), la ecuación de la parábola referida a estos nuevos ejes es:
y como las ecuaciones de la translación de ejes son:
la ecuación de la parábola es
Además si efectuamos las operaciones indicadas, esta ecuación se representa por el trinomio de segundo grado
|
Mover el punto O¢ utilizando los botones que aparecen en la parte inferior de la ventana. También se puede colocar el puntero de ratón sobre O¢, pulsar el botón principal del ratón y, sin soltarlo, transladar el punto a una nueva posición. Al soltar el botón del ratón, el punto O¢ se sitúa en las coordenadas elegidas. |
|
Pulsar el botón limpiar para eliminar el rastro dejado por el punto O¢ en la translación. |
|
El punto Q está asociado al punto P por las ecuaciones de la translación. Al mover el punto P éste describe una parábola de vértice el origen de coordenadas, luego el lugar geométrico del punto Q también es una parábola. |
1. Hallar la ecuación de una parábola simétrico con respecto al eje OX cuyo vértice está en el origen de coordenadas y su parámetro es p = 3.
2. Hallar la ecuación de una parábola cuyo vértice está en el origen de coordenadas, sabiendo que:
i) la parábola es simétrica con respecto al eje de abscisas y pasa por el punto A(9, 6).
ii) la parábola es simétrica con respecto al eje OX y pasa por el punto A(– 1, 3).
3. Hallar el foco F y la ecuación de la directriz de la parábola y² = 24x.
4. Hallar la ecuación de una parábola siendo las coordenadas de su foco F(– 7,0) y la ecuación de la directriz r º x – 7 = 0.
5. Hallar la ecuación de una parábola, si se dan su foco F(7, 2) y la directriz r º x – 5 = 0.
6. Verificar que cada una de las ecuaciones siguientes determina una parábola y hallar las coordenadas de su vértice, la magnitud del parámetro p y la ecuación de la directriz:
i) y² = 4x – 8 ii) y² = 4 – 6x
 |
 |
 |
Autor: Antonio Berhó Rodríguez
 |
Alumno |
| Ministerio de Educación, Cultura y Deporte. Año 2001 | |
| Alumno |
