La denominación de cónicas según hemos visto se atribuye a las curvas que se obtienen por sección de un cono circular recto con planos. En el apartado se estudiaron las cónicas como lugares geométricos de puntos del plano. Hemos de observar que, a diferencia de la elipse y la hipérbola, en la noción de parábola hemos introducido un concepto nuevo, su directriz. La parábola puede ser definida como el lugar geométrico de los puntos del plano tales que la razón de las distancias al foco y a la directriz es una cantidad constante e igual a la unidad.
Sin embargo, la elipse y la hipérbola gozan también de esa propiedad. Para cada foco de la elipse o de la hipérbola se puede exhibir una dirección denominada directriz asociada tal que la razón de los radios vectores de los puntos de esas curvas y la distancias a la directriz asociada es una constante.
Este apartado está dedicado al estudio de esta propiedad de la elipse y de la hipérbola.
Definición: Una sección cónica o simplemente una cónica es el lugar geométrico de los puntos del plano cuya relación de distancias a un punto y una recta fijos es constante.
El punto fijo se llama foco, la recta fija directriz y la relación constante excentricidad que, normalmente, se representa por la letra e.
Teorema: El lugar geométrico de los puntos del plano tales que la razón constante e de la distancia a un punto y una recta fijos es una elipse si e < 1 y una hipérbola si e > 1.
Demostración: Probaremos que en un sistema de referencia debidamente elegido, el lugar geométrico del plano que verifican las condiciones del enunciado esta definido por las ecuaciones:
|
si e < 1, es decir, es una elipse |
|
si e > 1, es decir es, una hipérbola |
Establezcamos un sistema de referencia cuyo eje OX coincida con la recta que pasa por el foco F y es perpendicular a la directriz r, con un origen O todavía no determinado. Sea p la distancia del foco a la directriz, la cual suponemos conocida. Introduzcamos ahora la variable c, distancia del origen de coordenadas al foco, c = OF. En este sistema de referencia las coordenadas del foco son F (c, 0) y la ecuación de la directriz r º x – (c + p) = 0.
Sea P (x, y) un punto cualquiera del plano, la relación
|
[1] |
es una condición necesaria y suficiente para que P pertenezca a la sección cónica. Por las fórmulas de la distancia entre dos puntos y la distancia de un punto a una recta se tiene
|
|
[2] |
De [1] y [2] se sigue la relación
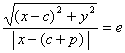
es una condición necesaria y suficiente para que el punto P pertenezca a la cónica. Eliminando el radical se obtiene la igualdad
|
[3] |
Esta expresión no constituye la ecuación de una cónica apuesto que se ha escogido de un modo especial el sistema de referencia.
Si e ¹ 1 basta tomar el origen O de manera que c = e² p/(1 – e²) y orientar el eje de abscisas de O hacia F, con ello la relación [3] se puede escribir en la forma
|
[4] |
Ahora será necesario efectuar la distinción de las dos posibilidades que ofrece la excentricidad e, de ser mayor o menor que 1. Al poner a = e p/(1 – e²) para el denominador y² se tienen dos posibilidades
| si e < 1 entonces | si 1 < e entonces |
y por consiguiente se tendrán dos tipos de cónicas, cuyas ecuaciones serán:
|
|
elipse |
e < 1 |
(en la que a = b corresponde a la ecuación de una circunferencia), y
|
|
hipérbola |
1 < e |
![]()
|
1. Hallar la ecuación de una elipse cuyos focos están en el eje de abscisas y son simétricos con respecto al origen de coordenadas sabiendo, además, que:
i) la distancia entre sus focos es 6 y la excentricidad 3/5.
ii) su eje mayor 2a es igual a 20 y la excentricidad 3/5.
iii) su eje menor 2b es igual a 10 y la excentricidad 12/13.
iv) la distancia entre sus directrices es igual a 5 y la distancia entre sus focos 4.
v) la distancia entre sus directrices es igual a 32 y la excentricidad 1/2.
2. La excentricidad de una elipse es 2/3 y el radio vector de un punto P de la misma es igual a 10. Calcular la distancia del punto P a la directriz asociada a dicho foco. Representar la elipse con ayuda del applet anterior.
3. La excentricidad de una elipse es 2/5 y la distancia de un punto P de la misma a una directriz es 20. Calcular la distancia del punto P al foco asociado a la directriz.
Observación 1: La excentricidad de una elipse puede entenderse como la medida de su aplastamiento.
![]()
|
Observación 2: Si e < 1 entonces el foco se halla entre el origen y la directriz, que tiene por ecuación x = a/e. Además por la simetría de la curva existe otro foco y otra directriz.
![]()
|
1. Hallar la ecuación de una hipérbola cuyos focos están en el eje de abscisas y son simétricos con respecto al origen de coordenadas, sabiendo, además, que:
i) la distancia entre los focos es 10 y el semieje menor 2b es igual a 8.
ii) la distancia entre los focos es 6 y la excentricidad 3/2.
iii) la distancia entre las directrices es igual a 32/5 y el eje menor 6.
iv) la distancia entre las directrices es igual a 8/3 y la excentricidad 3/2.
2. La excentricidad de una hipérbola es 3 y la distancia de un punto P de la misma a la directriz es igual a 4. Calcular la distancia del punto P al foco asociado a esa directriz. Representar la hipérbola.
3. La excentricidad de una hipérbola es , su centro está en el origen de coordenadas y uno de los focos tiene por coordenadas F (12, 0). Calcular la distancia del punto P de la hipérbola, de abscisas igual a 13, a la directriz correspondiente al foco dado.
Observación 3: Si 1 < e entonces la directriz se halla entre el foco y el origen. Por la simetría de la curva existe otro foco y otra directriz, de ecuaciones x = a/e y x = – a/e.
Observación 4: Si e = 1 entonces el origen del sistema de referencia se situaría en el punto medio del segmento FD con lo cual resultará la ecuación de una parábola.
Autor: Antonio Berhó Rodríguez
| Alumno | |
| Ministerio de Educación, Cultura y Deporte. Año 2001 | |
| Alumno |