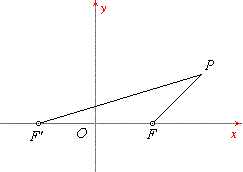
|
|
|
Para obtener la
ecuación canónica o ecuación reducida de la elipse situemos un sistema de coordenadas
cartesianas con origen O en el punto medio del segmento FF¢ y eje de abscisas en la dirección de la recta que
une los focos. En este sistema de referencia las coordenadas de los focos son F
(c, 0) y F¢ (–
c, 0). Si ahora P (x, y) es un punto
cualquiera de la elipse aplicando la fórmula de la distancia entre dos puntos:
|
|
[2] |
De [1] y [2] resulta que la relación
|
[3] |
es una condición necesaria y suficiente para que el punto P (x, y) esté situado en la elipse. Eliminando los radicales después de elevar al cuadrado y simplificar los términos semejantes se llega a la ecuación
|
[4] |
donde hemos puesto b² = a² – c².
Las coordenadas de todo punto P (x, y) de la elipse satisface la ecuación [4] obtenida de la ecuación [3]. Pero como toda transformación algebraica ligada a la eliminación de radicales es susceptible de hacer aparecer raíces extrañas, debemos asegurarnos que todo punto P cuyas coordenadas x e y satisfacen la ecuación [4] está sobre la elipse. Para ello es suficiente demostrar que los radios vectores segmentos PF y PF¢ de todo punto P verifican la condición [1]. Supongamos entonces que las coordenadas de un punto P (x, y) satisfacen la ecuación [4]. Despejando y² en [4] y sustituyendo en la expresión [2] de PF, se obtiene, después de unos cuantos cálculos elementales:
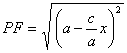
y como el radicando es positivo, se concluye que
De forma análoga se establece que
Por lo tanto, para el punto P considerado se tiene que
|
|
es decir
y el punto P considerado se encuentra sobre la elipse. La ecuación [4] se denomina ecuación canónica de la elipse.
Como la ecuación [4] sólo contiene potencias pares de las variables x e y, la curva es simétrica con respecto a los ejes de coordenadas, y con respecto al origen. El punto O es el centro de la elipse.
Si transladamos los ejes paralelamente de forma que el origen sea el punto O¢(h, k) resulta que la ecuación de la elipse referida a estos ejes, es según hemos demostrado antes
Como las ecuaciones de la translación son
la ecuación de la elipse es
|
Mover el punto O¢ utilizando los botones que aparecen en la parte inferior de la ventana. También se puede colocar el puntero de ratón sobre O¢, pulsar el botón principal del ratón y, sin soltarlo, transladar el punto a una nueva posición. Al soltar el botón del ratón, el punto O¢ se sitúa en las coordenadas elegidas. |
|
Pulsar el botón limpiar para eliminar el rastro dejado por el punto O¢ en la translación. |
|
El punto Q está asociado al punto P por las ecuaciones de la translación. Al mover el punto P éste describe una elipse de centro el origen de coordenadas, luego el lugar geométrico del punto Q también es una elipse. |
1. Trazar las elipses de centros los puntos O¢(–1, 2), O¢(3, –2), O¢(2, 3) y O¢(–4, –3), indicando en cada caso las coordenadas de los focos.
2. Escribir la ecuaciones canónicas de las elipses del ejercicio anterior.
 |
 |
 |
Autor: Antonio Berhó Rodríguez
 |
Alumno |
| Ministerio de Educación, Cultura y Deporte. Año 2001 | |
| Alumno |
