

VECTORES EN EL PLANO
12.- Producto escalar de vectores.
Dados dos vectores a y b definimos el producto escalar de ambos como : a.b = |a|.|b|cos (a,b)
|
|
Modifica los puntos A y B en la escena o en los controles numéricos, obtendrás el producto escalar de los vectores y el ángulo que forman. |
13.- Propiedades del producto escalar.
| a.b = b.a |
| a.a>=0 |
| a.(b+c)=a.b+a.c |
| k(a.b) = (k*a).b |
14.- Interpretación geométrica del producto escalar.
El producto escalar de dos vectores es igual al módulo de uno de ellos por la proyección del otro sobre él.
| INTERPRETACIÓN GEOMÉTRICA DEL PRODUCTO
ESCALAR
|
Altera la posición de los puntos y observa los resultados que vas obteniendo. |
Dados dos vectores a = ax i+ayj y b = bxi+byj el producto escalar de a.b se obtiene de la siguiente forma: a.b = ax.bx+ay.by
|
|
a.b= (ax i+ayj).(bxi+byj) =ax ibxi+ax ibyj+ayjbxi+ayj+byj =axbx+ayby |
Dado un vector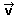 se verifica que
se verifica que
![]() .
.
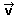 .
.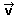 =|
=|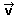 |.|
|.|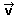 |.cos
0º = |
|.cos
0º = |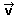 ||
||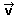 | , si
despejamos el módulo de
| , si
despejamos el módulo de 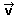 obtenemos la fórmula
anterior.
obtenemos la fórmula
anterior.
A partir de la expresión del producto escalar podemos determinar el ángulo de dos vectores despejando su coseno en la fórmula del producto escalar:
cos(a,b) = a.b/|a|.|b|
| |||||||||||||||

Los contenidos de esta unidad didáctica están bajo una licencia de Creative Commons si no se indica lo contrario.