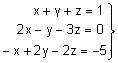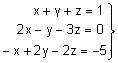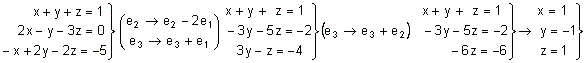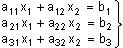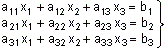OTROS SISTEMAS DE ECUACIONES LINEALES

A) Sistemas de tres ecuaciones con dos incógnitas:

Resolver este sistema equivale geométricamente a determinar la posición relativa de tres rectas en el plano. Estos sistemas se resuelven considerando un subsistema de dos cualesquiera de sus ecuaciones y comprobando la verificación, o no, de la solución en la tercera ecuación.

B) Sistemas de tres ecuaciones con tres incógnitas:

Para su resolución se utiliza el método de Gauss, transformando el sistema en otro equivalente y triangular.

Ejemplos

A) Resolver los sistemas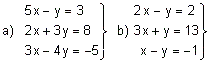

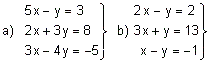
a)	En el primer sistema, resolviendo cualquier subsistema de dos ecuaciones nos da la solución (1,2), es decir, las tres rectas se cortan en el mismo punto, por lo tanto, el sistema es compatible: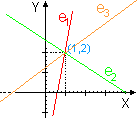
b)	En el segundo sistema, si elegimos un subsistema de dos ecuaciones, tiene una solución que no verifica la tercera ecuación, es decir, las rectas se cortan dos a dos pero no tienen punto alguno común a las tres, por lo tanto, el sistema es incompatible: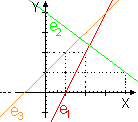

B) Resolver el sistema

Ficha 6