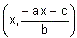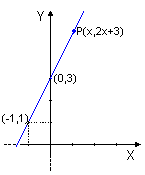ECUACIÓN DE 1^er GRADO(LINEAL) CON DOS INCÓGNITAS

Son aquellas que se pueden expresar directamente, o aplicándole transformaciones de equivalencia, de la forma:

ax + by + c = 0, con a0 y b0.

• Resolver dicha ecuación es encontrar los pares (x,y) que verifican la igualdad.
• Como b0, podemos despejar y de la ecuación y obtenemos así otra ecuación equivalente de la forma y=mx+n; ecuación que corresponde con la expresión algebraica de las funciones afines, y cuya representación gráfica es una recta de pendiente "m" y ordenada en el origen "n".
  Por lo tanto, los pares (x,y) que son solución de la ecuación lineal ax+by+c=0, son las coordenadas de los puntos de la recta cuya ecuación es y=mx+n;es decir son los pares indeterminados de la forma

EJEMPLO

Resuelve la ecuación: 2x - y + 3 = 0

• La solución algebraica viene dada por el par ordenado (x,2x+3), solución general.
  Es una solución indeterminada, que para cada valor concreto de x nos da un valor respectivo de y, obteniéndose así una de las infinitas soluciones indicadas por el anterior par ordenado. Así si x = -2, y valdrá y=2·(-2)+3=-1, es decir, (-2,-1), es una solución particular.

la solución geométricca es la recta formada por los puntos que tiene por coordenadas los infinitos pares anteriores(a la ecuación anterior, se le llama ecuación de la recta):

Puedes ver en esta escena que cualquier recta siempre tiene una ecuación lineal asociada.

Puedes desplazar los puntos A y B arrastrándolos con el ratón. El parámetro coord. enteras permite alternar entre moverse por coordenadas enteras o decimales.

Ficha 3