RESOLUCIÓN DE TRIÁNGULOS RECTÁNGULOS
Resolver un triángulo consiste en calcular seis elementos: los tres lados y los tres ángulos. Para ello necesitamos conocer tres de estos seis elementos y uno de los datos por lo menos sea un lado. Si el triángulo es rectángulo (un ángulo es 90º) basta conocer dos de sus elementos, uno de los cuales debe ser un lado.
Se llama razón trigonométrica de un ángulo agudo a cada uno de los cocientes que se pueden establecer entre los lados de un triángulo rectángulo cualquiera.Las razones trigonométricas fundamentales (seno, coseno y tangente) relacionan los ángulos agudos y los lados de un triángulo rectángulo de la siguiente forma:
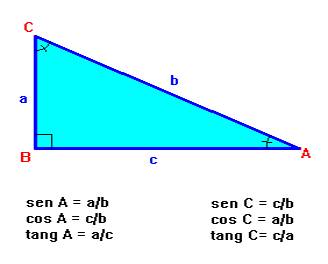
Los lados de un triángulo rectángulo verifican el teorema de ![]() Pitágoras :
Pitágoras :
Para hallar los ángulos se utilizan las inversas de seno, coseno y tangente de la siguiente forma:
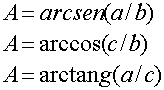 |
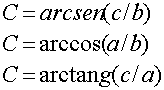 |
Utilizando dichas relaciones se pueden calcular los elementos desconocidos a partir de los conocidos.
Se pueden dar dos casos:
-Se conocen dos lados del triángulo.
I.- Un cateto y la hipotenusa
II.-Los dos catetos
-Se conoce un lado y un ángulo agudo del triángulo.
III.-Un ángulo agudo y un cateto
IV.- Un ángulo agudo y la hipotenusa
I.- Un cateto y la hipotenusa
1.-Varía el valor de la hipotenusa hasta que valga 6 y el otro cateto valga 3.Fíjate cuánto valen los ángulos agudos B y C.
2.-Fíjate en las medidas de los lados del triángulo rectángulo inicialmente. Sus lados miden exactamente 3 , 4 y 5.Es decir, verifican el teorema de Pitágoras:
![]()
Tres números naturales en estas condiciones se denominan terna pitagórica. Calcula tú otra terna pitagórica.
3.-Resuelve el triángulo rectángulo ABC en los siguientes casos:
a) Cateto 2.5 cm e hipotenusa 3.5 cm .
b) Hipotenusa 10 cm y cateto 5 cm .
4.- Calcula el coseno del ángulo C sabiendo que un cateto vale 5 y que la hipotenusa 13.
5.- Una escalera de 3 metros se apoya en la pared alcanzando una altura de 2 metros.¿Qué ángulo forma la escalera con el suelo?
6.- La longitud de un trozo de carretera es de 450 metros y la diferencia de altura entre los extremos de la carretera es 70 metros.¿Cuál es la inclinación de este trozo de carretera?
II.-Los dos catetos
7.-Varía el valor de los catetos hasta que ambos valgan 4. ¿Cuánto miden los ángulos agudos del triángulo rectángulo?. Considera ahora los catetos iguales a 6.¿Cuánto miden ahora?,¿Cómo se llaman estos triángulos? ¿Qué se deduce de ello?
8.-Resuelve el triángulo rectángulo ABC en los siguientes casos:
q Que tenga por catetos 3.5 cm y 5 cm.
q Que tenga por catetos 6 cm y 8.7 cm.
9.- Calcula el coseno del ángulo C sabiendo que los catetos a y c mide 150 metros y 360 metros, respectivamente.
|