Punto simétrico de un puntos respecto de
otro
Consideremos el punto A(x1,
y1) y el punto B(x2, y2). Vamos a calcular el punto simétrico C(x3, y3) de A respecto
de B. Para ello, vamos a tener en cuenta que el punto B será el punto medio de
A y C. Teniendo en cuenta el apartado
anterior, se cumple:
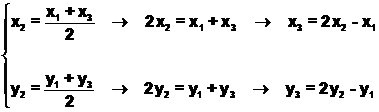
Expresiones que nos permiten calcular el simétrico de A
respecto de B en función de sus coordenadas.
1. Halla las coordenadas del punto simétrico de A(4, -1)
respecto de B(7, -2). Comprueba si la solución coincide con la obtenida en tu
cuaderno de trabajo.
2. Si M(-3, 5) es el punto medio del segmento AB, halla
el punto B si A(6, -4). ¿Se cumple que la distancia de A a M es igual a la
distancia de M a B?. ¿Qué relación existe entre los segmentos de color verde,
azul y rojo?
3. Dados los puntos A(0, 4) y B(-5, 0), halla el punto
simétrico de A respecto de B y el simétrico de B respecto de A. Comprueba la
solución obtenida con la obtenida en tu cuaderno de trabajo.
Condición para que tres puntos estén alineados
|
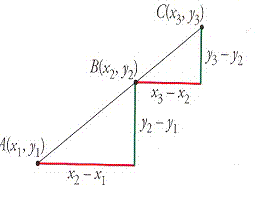
Si los tres puntos A(x1, y1),
B(x2, y2) y C(x3, y3) estén
alineados, entonces los dos triángulos señalados son semejantes y, por tanto,
sus lados son proporcionales. Aplicando las propiedades de la
semejanza de triángulos se obtiene:
Esta es la condición para que los tres
puntos estén alineados. |
|
1.
Comprobar si los puntos A(2, -1), B(6, 1) y C(8, 2) están
alineados. Comprobarlo en vuestro cuaderno de trabajo.
2.
Comprobar si los puntos A(-3, -3), B(6, 5) y C(8, 7)
están alineados. Comprobarlo en vuestro cuaderno de trabajo.
3.
Calcular m para que los puntos A(5, -2), B(-1, 1)
y C(2, m) estén alineados. ¿Es posible determinar m utilizando la escena
anterior?.
Ecuación de la recta que pasa por dos puntos
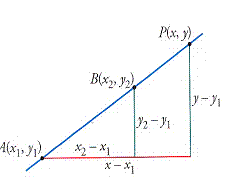
Dados los puntos A(x1, y1) y B(x2, y2)
y consideremos la recta que pasa por estos puntos. Si tomamos un punto
genérico de la recta, P(x, y), éste está alineado con A y B. Por tanto, los
dos triángulos rectángulos son semejantes.
Aplicando las propiedades
de la semejanza de triángulos se obtiene:
|
|
1.
Hallar la ecuación de la recta que pasa por los puntos
A(-3, 4) y B(5, -1). Comprueba que el resultado coincide con el obtenido en tu
cuaderno de trabajo.
2.
Hallar la ecuación de la recta que pasa por los puntos:
a) A(5, -1) y B(5, 7). b)
A(-2, 6) y B(7, 6). (Observa que esta
fórmula no sirve cuando los puntos tienen la misma abscisa o la misma ordenada.
En ambos casos, la recta es paralela al eje X o al eje Y, y su ecuación es muy
sencilla).
3.
Dado el triángulo de vértices A(-2, 1), B(4, 7) y C(10,
-5). Halla las ecuaciones de las rectas sobre las que están situados los lados.
4.
Halla la ecuación de la recta que pasa por el punto A(4,
-2) y su pendiente m = -2.
|