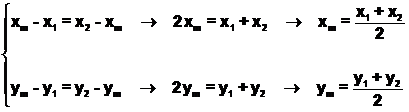RELACIONES ANALÍTICAS ENTRE PUNTOS ALINEADOS
Introducción
Los
recursos presentados en esta unidad centran especialmente su atención en la forma
de valorar el grado de adquisición de las competencias básicas. Para su
elaboración, se han utilizado aquellos elementos que se consideran
imprescindibles para realizar un estudio posterior de la recta en el plano, así como de las posiciones
relativas de las rectas, que se imparte en Matemáticas en el curso 4º de
Educación Secundaria Obligatoria, tanto en las Básicas como en las Ampliadas.
En
esta Unidad Didáctica se hace una introducción a la geometría analítica del
plano, estudiando la representación gráfica de puntos y segmentos, punto medio
de un segmento, punto simétrico de un punto respecto de otro, alineación de
puntos y distancia entre dos puntos.
Objetivos
1. Manejar gráfica y analíticamente los puntos del plano
y establecer relaciones entre ellos.
2. Obtener razonadamente el punto medio de un segmento o
los puntos mediante los que un segmento queda partido en tres (o más) trozos
iguales.
3. Aplicar el cálculo de la distancia entre dos puntos
para determinar las dimensiones de figuras poligonales representadas en un
sistema de coordenadas.
4. Determinar la condición que deben cumplir tres puntos
para que estén alineados.
5. Calcular la ecuación de la recta que pasa por dos
puntos.
Representación gráfica de puntos y segmentos
La representación gráfica de un punto en el plano
viene dada por sus dos coordenadas: la primera coordenada se llama abscisa y la segunda ordenada. Entonces, un
punto cualquiera se expresa de la forma siguiente: P(x,y).
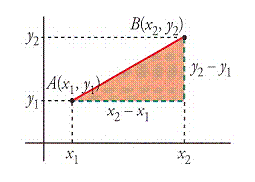
Consideremos los puntos A(x1,y1)
y B(x2,y2) en el plano cartesiano y, a continuación,
trazamos el segmento determinado por dichos puntos que representaremos por la
notación: AB.
1.
Representar los
puntos A(1,7) y B(5,-3) utilizando el ratón del ordenador desplazando los
puntos A y B de la escena. A continuación, pulsa Inicio, y represéntalos de
nuevo utilizando los controles de escenas.
2.
Representa, en tu
cuaderno de trabajo, los siguientes puntos: A(3,1), B(-5,3), C(1,2), D(-1,-2),
E(-2,-3), F(5,0) y halla los segmentos AB, CD y EF . A continuación, utiliza la
escena para su comprobación.
3.
Utiliza los
controles zoom para ampliar o disminuir la cuadrícula de la escena, y los
controles O.x y O.y para desplazar los ejes, si fuera necesario, para
representar puntos que no puedan representarse con la configuración inicial.
Distancia entre dos puntos
|
Dados dos puntos cualesquiera, A(x1,
y1) y B(x2, y2), su distancia se obtiene
aplicando el teorema de Pitágoras, en el triángulo coloreado. Está fórmula también es válida si los
puntos tienen la misma abscisa y la misma ordenada. |
|
1.
Halla la
distancia entre los puntos A(-2, 2) y B(6, 4). Comprueba en tu cuaderno de
trabajo si la solución coincide con el resultado obtenido en la escena.
2.
Calcular los
lados del triángulo de vértices A(-2, 2), B(1, 6) y C(6, -6).
3.
En tu cuaderno,
representa los puntos A(-2, 3), B(-3, -1), C(4, -2) y D(2, 4) y calcula la
longitud de los segmentos AB y CD. Comprueba la solución en la escena.
4.
Calcula el valor
de c para que el punto A(10, c) diste 13 unidades del punto B(-2, 5).
¿La solución es única?
Punto medio de un segmento
|
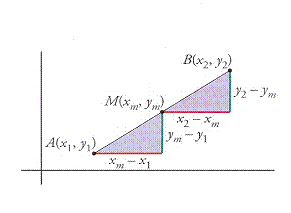
Consideremos un segmento de extremos A(x1,
y1) y B(x2, y2). Representaremos su punto medio por M(xm, ym) y
queremos hallar las coordenadas de M en función de A y B.
Observando la figura adjunta se debe cumplir que los dos triángulos
rectángulos deben ser iguales. Por lo tanto:
|
|
Las coordenadas
del punto medio de un segmento son la semisuma de las coordenadas de sus
extremos.
El punto medio de un segmento equidista
de los extremos.
1. Halla las coordenadas del punto medio del segmento de
extremos A(-2, 5) y B(4, 1). Comprueba el resultado con el obtenido en tu
cuaderno de trabajo.
2. Halla las coordenadas de los puntos medios de los
lados de un triángulo cuyos vértices son: A(1, 7), B(5, -3) y C(-6, -1).
3. Dado el cuadrilátero ABCD cuyos vértices son los
puntos A(4, 6), B(-2, 3), C(-4, -4) y
D(6, -2). Calcula las coordenadas de los puntos medios de los lados y de las
diagonales.
4. a) Halla el
punto medio del segmento de extremos A(-2, 0) y B(6, 4). b)
Comprueba que la distancia del punto medio a cada uno de los extremos es
la misma. (Sugerencia: utiliza la segunda
escena para este último apartado)
|