FUNCIÓN REAL DE VARIABLE REAL
	Análisis

1. DEFINICIÓN
Toda aplicación de un subconjunto de los números reales en el conjunto se denomina función real de variable real.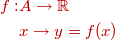 El subconjunto  constituye el dominio de la función, es decir, el conjunto de valores reales que tienen imagen por . El conjunto de imágenes por  es un subconjunto de  que se denomina recorrido o imagen de la función. En un sistema de ejes de coordenadas en el plano, el conjunto de todos los puntos 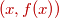, con , constituye la gráfica de la función . En la gráfica de una función, el dominio se representa sobre el eje horizontal, OX, mientras que la imagen o recorrido se representa sobre el eje vertical, OY. A continuación analizaremos el dominio de algunos tipos de funciones: Están definidas en  las funciones polinómicas, las funciones trigonométricas, , , y también la función irracional , con n impar. Ejemplos: Las funciones racionales, , están definidas en todos los puntos en que el denominador, , no se anula. Ejemplos: Si los valores que anulan el denominador son las soluciones de la ecuación: Si Si . Las funciones cociente de funciones no polinómicas, , están definidas para todos los valores de x en los que y están definidas a la vez, excepto en aquellos para los que se anula . La funciones  exponenciales, y , con ; están definidas para todos los valores de x en los que está definida. Ejemplo: , puesto que la función del exponente es una función polinómica. Las funciones logarítmicas, y , están definidas para . Ejemplo: Si que son las soluciones de . La función tangente, no está definida en los puntos en los que . Las funciones irracionales, , con n par, están definidas para . Ejemplos: Si  que son las soluciones de la inecuación . Si pues son las soluciones de .
Esta unidad interactiva requiere la máquina virtual de Java J2RE.	1.- Ayudándote de la escena, estudia el dominio de las siguientes funciones: En la siguiente escena tienes representadas las funciones del ejercicio anterior para que te sirvan de guía a la hora de realizar el jercicio. Con el control  Ejemplos Dominios Funciones puedes moverte de una función a otra. Fíjate que le ocurre a la gráfica de la función en los puntos en los que no está definida. 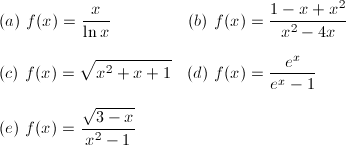2.- En el siguiente enlace tienes una relación de ejercicios resuelta sobre el cáculo del dominio de una función: relación de ejercicios.

	Mª del Carmen Torres Alonso
	© Ministerio de Educación. Año 2011

Los contenidos de esta unidad didáctica están bajo una licencia de Creative Commons si no se indica lo contrario.