1. Si 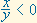, entonces el punto P(x,y) :

A. Pertenece al segundo cuadrante.
B. Pertenece al cuarto cuadrante
C. Pertenece al segundo o al cuarto cuadrante.
D. Ninguna de las respuestas anteriores es correcta.

2. Dado el punto P(x,y), se verifica:

A. d(P,OX) = x.
B. d(P,OX) = |x|.
C. d(P,OX) = y.
D. d(P,OX) = |y|

3. Los puntos que cumplen y = -3 representan:

A. Una recta horizontal.
B. Una recta vertical.
C. Una recta inclinada.
D. Ninguna recta, pues y = -3 es la solución de una ecuación.

4. La ecuación 5x - 2y = 2

A. Tiene infinitas soluciones en el segundo cuadrante.
B. No tiene soluciones en el segundo cuadrante.
C. Tiene infinitas soluciones en los cuadrantes segundo y cuarto.
D. Ninguna de las respuestas anteriores es correcta.

5. La recta solución de la ecuación 4x - 3y = -36 determina con los ejes cartesianos un triángulo:

A. De perímetro 36 y área 54.
B. De perímetro 36 y área 45.
C. De perímetro 63 y área 45.
D. De perímetro 54 y área 63.

6. Hallar el valor del parámetro k para que la recta 3kx + 5y + 7 = 0 pase por el punto (-1,4).

A. k = -9.
B. k = 0.
C. k = 9.
D. k = 1.

7. Hallar el valor de k para que la recta de ecuación kx + 3y + 6 = 0 forme con los ejes coordenados un triángulo de área 2 unidades de superficie.

A. k = 0.
B. k = -3.
C. k = 3.
D. k = 13.

8. El sistema de ecuaciones lineales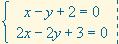

A. Es compatible determinado.
B. Es compatible indeterminado.
C. Es incompatible.
D. No es lineal.

9. Las coordenadas de los vértices del triángulo cuyos lados están sobre las rectas r: 3x - y - 4 = 0, s: 3x - 4y + 11 = 0, t: 3x + 2y - 1 = 0, son:

A. (3,5), (1,-1) y (-1,2).
B. (3,-5), (1,-1) y (-1,2).
C. (-3,-5), (1,-1) y (-1,2).
D. (-3,5), (1,-1) y (-1,2)

10. La solución analítica de un sistema indeterminado:

A. Se expresa con ecuaciones paramétricas.
B. Se escribe en la tabla de valores.
C. Se representa gráficamente.
D. Un sistema indeterminado no tiene solución.