1.
INECUACIONES
Una inecuación es una desigualdad entre expresiones algebraicas, tal que, su verificación depende de los valores de las variables que en ella intervienen.Por ejemplo,
Toda desigualdad viene determinada por uno de los signos de relación siguientes: <, £, > ó ³. Que admiten las siguientes transformaciones de equivalencia:
si a<b,"c, a+c < b+c y a-c < b-c.
Es decir, si en los dos miembros de una desialgualdad sumamos, o restamos, un número real cualquiera obtenemos otra desigualdad equivalente con el mismo signo de desigualdad.
si a<b, "c>0, a·c < b·c y.
Es decir, si los dos miembros de una desigualdad se multiplican, o dividen, por un mismo número real positivo, resulta otra desigualdad equivalente a la dada con el mismo signo de desigualdad.si a<b, "c<0, a·c > b·c y.
Es decir, si los dos miembros de una desigualdad se multiplican, o dividen, por un mismo número real negativo, resulta otra desigualdad equivalente a la dada, pero cuyo signo de desigualdad es de sentido contrario a la dadaResolver una inecuación es encontrar todas las solución, es decir, encontrar los valores de la variable que la verifican.
El proceso de resolución se basa en tranformaciones de equivalencia hasta llegar a una inecuación en la que la incógnita este sólo en uno de sus miembros y como único termino de este miembro, x<s . La solución viene dada por los infinitos valores que verifican esta última desigualdad, es decir, la semirrecta(intervalo) que tiene por origen al valor s:
- Por ejemplo, resolver
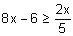
- multiplicamos los dos miembros de la desigualdad por 5, obtenemos así la inecuación equivalente:
- restamos en los dos miembros 2x, obtenemos:
- sumamos en ambos miembros 30:
- dividimos los dos miembros por 38:
.
Por lo tanto la solución es la semirecta; gráficamente sería:
Veamos ahora, en la siguiente escena, la resolución gráfica de una inecuación de primer grado con una incógnita.
Para hacer el estudio gráfico, expresamos la inecuación dada mediante otra equivalente de la forma ax+b<0 (el signo de la desigualdad será el que se nos dé en la inecuación que nos propongan):
Para resolver la inecuación
0, para escribir < 1, para escribir £ (en la escena se escribe < =) 2, para escribir > 3, para escribir ³ (en la escena se escribe > =)
Si te fijas sólo en el eje X verás una recta así: ____________________________________
El trozo azul corresponde a los valores de x que hacen el polinomio positivo, el naranja los que lo hacen negativo y el punto de unión lo hace cero.
Si muves el punto P con el ratón, puedes observar el signo del polinomio 38x -30. Y comprobar, en su caso, qué valores de x son solución de la inecuación. La semirrecta solución viene marcada en la escena por
Recuerda que si hay igualdad en el signo de relación, el intervalo es cerrado por ése extremo, y si no la hay, es abierto.
EJERCICIO:
Resuelve en tu cuaderno de trabajo las inecuacones:
a) 3 x + 6 > 0; b) 2 x - 4 £ 0; c) 5 x + 2 ³ 0
Para cada una de las inecuaciones anteriores, cambia en la escena los valores de a, b y el signo de relación y comprueba los resultados que has obtenido.SISTEMAS
Un sistema de inecuaciones de primer grado, con una variable, es un conjunto de dos o más inecuaciones con la misma variable.
La solución es el conjunto de números reales que verifica, a la vez, a todas las inecuaciones. Para hallarla, se resuelve por separado cada una de las inecuaciones y, después, se consideran sólo las soluciones comunes a todas ellas.
Veamos ahora, en la siguiente escena, la resolución gráfica de un sistema de dos inecuaciones lineales con una incógnita.
Para hacer el estudio gráfico, expresamos las dos inecuaciones mediante otras equivalente de la forma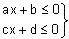
(el signo de la desigualdad será el que se nos dé en las inecuaciones que nos propongan):
Vamosa resolver el sistema:
- la primera inecuación esta expresada con los controles a, b y rel:1ª
- la segunda inecuación está expresada con los controles c, d y rel:2ª
- la solución del sistema se representa en la gráfica inferior de la escena. Si muves el punto P con el ratón, puedes observar el signo de los dos polinomios; así como, que se verifican, simultáneamente, sólo en el intervalo solución(de color verde).
Resuélvelo en tu cuaderno de trabajo y comprueba los resultados que aparecen en la escena. Si lo necesitas, cambia la escala o desplázate por la Recta real.
EJERCICIO:
Resuelve en tu cuaderno de trabajo los sistemas:
a); b)
; c)
Para cada uno de los sistemas, cambia en la escena los valores de a, b, c, d y los respectivos signos de relación y comprueba los resultados que has obtenido.
Diego González Álvarez
Ministerio de Educación, Cultura y Deporte. Año 2005
