
 |
FUNCIÓ EXPONENCIAL |
| Definició i propietats. | |
| 1. DEFINICIÓ DE LA FUNCIÓ y = ax | |||||||||||||||||||||||||||||||||||||||||||||||
|
Una funció exponencial és del tipus f(x)=ax o y=ax, en què a és un nombre real positiu (a>0). |
|||||||||||||||||||||||||||||||||||||||||||||||
1.- Estudia la funció y=2x. Observa la representació de la successió de punts i utilitza l'escena per fer una taula de valors.
2.- Fes el mateix per a les altres bases de la taula següent.
3.- Observa que passa quan a=1. Té sentit per a=0? Què passa quan x=0? Per què? |
|||||||||||||||||||||||||||||||||||||||||||||||
| 2. REPRESENTACIÓ GRÀFICA I PROPIETATS DE LA FUNCIÓ y = ax | ||||||||||||
|
La gràfica de la funció y=ax depèn del valor de a. |
||||||||||||
1. Comprova gràficament que, independentment del valor de a, les gràfiques sempre passen pel punt (0,1). Per què? Sempre estan per sobre de l'eix d'abscisses? Per què? 2. Fes que es representi la funció y=5x; escriu els valors de 5-10, 5-2, 50, 53, 54,2 i 56,1. Observa que a mesura que augmenta l'exponent x, també augmenta el valor de la potència. Fes el mateix amb la funció exponencial y=(1/5)x. Passa el mateix? Prova-ho per a diferents valors de a. 3. Activa el rastre (r=1). Si a>1, que passa amb les funcions y=ax, a mesura que augmenta la base a? I si 0 < a < 1, com varien les funcions exponencials respecte de les variacions de a? 4. Representa la funció y=3x. Amb la teva calculadora científica, completa la taula següent:
Com evolucionen els valors de la potència? Quin creus que seria el valor de la potència pels exponents -100, -1000, -10000? Fes el mateix per a la funció y=(1/3)x, per a valors positius molt grans de l'exponent. |
||||||||||||
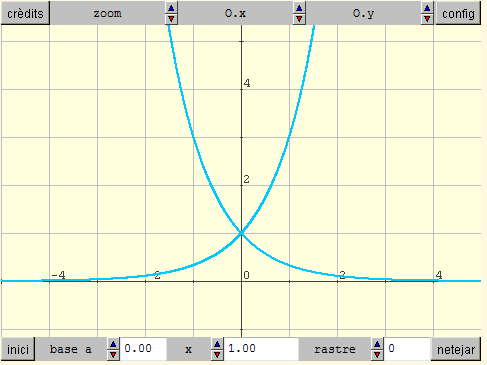 |
5. Intenta aconseguir aquesta imatge (o una de semblant). Les funcions y=ax i y=a-x =(1/a)x són simètriques respecte l'eix d'ordenades? Per què? |
|||||||||||
Propietats de la funció exponencial:
|
||||||||||||
| 3. TRANSLACIONS DE LA FUNCIÓ EXPONENCIAL. | ||
|
Les funcions y=ax+h són de tipus exponencial. Són iguals que la funció y=ax, i les obtenim traslladant la gràfica y=ax verticalment, h unitats cap amunt si h és positiu, i h unitats cap avall si és negatiu. Les funcions y=ax+k són també de tipus exponencial. Són iguals que la funció y=ax, i les obtenim traslladant aquesta gràfica horitzontalment, k unitats cap a l'esquerra si k és positiu, i k unitats cap a la dreta si és negatiu. |
||
1.-Comprova-ho en l'escena. Observa el desplaçament del punt (0,1).
2.-Representa la gràfica de la funció y=3x. Fes que es representin les funcions: y=3x-2, y=3x+3, y=3x-2 i y=3x-3. 3.-Fes el mateix amb la funció y=(1/4)x i les trasllades següents: y=(1/4)x-2, y=(1/4)x+3, y=(1/4)x-2 i y=(1/4)x-3. 4.-Representa en el teu quadern les següents funcions: y=-3+4x-5, y=5+2x-3, y=2+2x+2, y=-2+3x-1 y=-3+(1/4)x-5, y=5+(1/2)x-3, y=2+(1/2)x+2, y=-2+3-x-1 |
||
| 4. CAS PARTICULAR: LA FUNCIÓ EXPONENCIAL y= exp(x) = ex | ||
Existeix un nombre, anomenat a vegades constant de Napier, el nombre e. El matemàtic escocés John Napier (1550-1617) el va introduir en els seus estudis sobre logaritmes, encara que la seva notació explícita va ser adoptada pel matemàtic suís Leonard Euler (1707-1783). En estudis posteriors coneixerem millor aquest important nombre. És un nombre irracional, el valor aproximat del qual és: e=2.71828182845904523532874..... Donada la importància d'aquesta funció, és convenient tenir clares la seva representació i propietats. |
||
1.-Comprova que la funció exponencial y=ex (o també y=exp (x)), compleix totes les propietats de les funcions exponencials amb base a>1. 2.-Fes el mateix amb la funció exponencial y=e-x (o també y=exp (-x)). Quant val 1/e? Recorda que 1/e=e-1, i per tant, la base és 0 < a < 1. |
||
| Joan Carles Fiol Colomar | ||
 |
||
| Ministerio de Educación, Cultura y Deporte. Año 2009 | ||
![]()
Los contenidos de esta unidad didáctica están bajo una licencia de Creative Commons si no se indica lo contrario.