1. APROXIMACIÓN DE UNA DISTRIBUCIÓN BINOMIAL POR UNA NORMAL

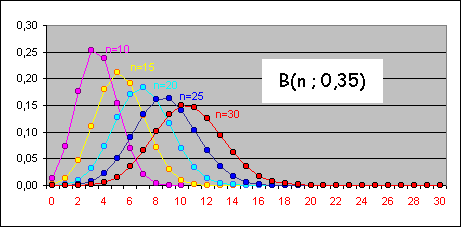
Una distribución binomial B(n,p) se parece a una normal tanto más cuanto mayor es el producto np (o nq si q<p, siendo q=1-p). Cuando np y nq superan 5, la aproximación es casi perfecta, como se puede apreciar en la figura.

En estas condiciones:

Podemos emplear la normal para calcular probabilidades en el caso de una distribución binomial, aunque hemos de tener en cuenta que la binomial es discreta y la normal continua, por lo que es necesario introducir un ajuste en el cálculo llamado corrección de Yates. Así:

p(X£x) = p(X'£x+0,5)          p(X<x) = p(X'£x-0.5)           p(X=x) = p(x-0,5£X'£ x+0,5)

Veamos un par de ejemplos:

1) El 35% de una población está afectado por la gripe. Se eligen 30 personas al azar.

Se trata de una B(30;0,35) que aproximamos por N(10,5;2,61)

Calcula la probabilidad de que:

• haya exactamente 10 enfermos

P(X=10) = P(9,5 £ X' £ 10,5)

• haya más de 5 y menos de 12 enfermos

P(5<X<12) = P(5,5£X'£11,5)

2. AJUSTE DE UN CONJUNTO DE DATOS A UNA NORMAL

Con frecuencia conviene saber si puede suponerse que una serie de datos obtenidos experimentalmente proceden de una población distribuida normalmente.

Recordemos que en una distribución normal:

• el 68% de los datos está en el intervalo (x-s, x+s)

• el 95% de los datos está en el intervalo (x-2s, x+2s)

• el 99% de los datos está en el intervalo (x-3s, x+3s)

Si calculadas la media x y la desviación típica s de nuestros datos, se cumplen aproximadamente estos porcentajes podemos considerar que la población de partida es normal. 

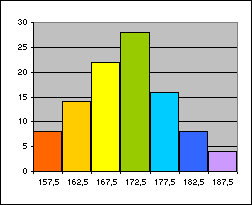
Veamos un ejemplo en el que seguimos un proceso un poco más elaborado:

Ejemplo

La tabla adjunta muestra la altura en cm de 100 estudiantes. ¿Es razonable suponer que estos resultados proceden de una distribución normal?

a) Calculamos la media y la desviación típica de la distribución

b) Comparamos la distribución empírica con la normal N((x,s) en este caso con la N(171;7,5).

• Tipificamos los extremos de cada intervalo y calculamos en cada caso

P(x_a<x£x_b)=P(z_a<z£z_b)

xa	xb	fri	za	zb	p(X<xa)	p(X<xb)	p(xa<X<xb)
155	160	0,08	-2,13	-1,47	0,0164	0,0712	0,05
160	165	0,14	-1,47	-0,80	0,0712	0,2119	0,14
165	170	0,22	-0,80	-0,13	0,2119	0,4470	0,24
170	175	0,28	-0,13	0,53	0,4470	0,7031	0,26
175	180	0,16	0,53	1,20	0,7031	0,8849	0,18
180	185	0,08	1,20	1,87	0,8849	0,9690	0,08
185	190	0,04	1,87	2,53	0,9690	0,9944	0,03
media			x= 171
desv. típica			s=7,50

Comparamos las probabilidades obtenidas con las frecuencias relativas y evaluamos las diferencias. En este caso, parecen suficientemente pequeñas como para aceptar que los datos provienen efectivamente de una distribución normal. 

Fíjate que este último paso es totalmente subjetivo, aunque existen métodos estadísticos con los que tomar esta decisión de forma más precisa.