3.-funciones exponenciales
Tenemos una gráfica de una
función
exponencial 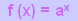 que podemos ir variando a
nuestro gusto usando el control a
de la escena.Puede tomar cualquier valor positivo distinto de 1Por ejemplo, representa en la gescena varias funciones exponenciales con a>1.¿Qué pasa al ir aumentando el valor de a? Copialas en tu cuaderno. Y ahora haz lo mismo pero con 0< a<1 a) Como son entre si, las gráficas de las funciones:
Y otra tabla similar a esta , para cuando la base es 1/2 |
|||||||||||||||||
| b)¿Cuál
es el dominio de todas las funciones que has representado?¿Y
el recorrido?Variaría algo la gráfica, su dominio o su recorrido, si
hago el valor absoluto de cualquiera de ellas? c)¿Corta alguna vez al eje de abscisas la función exponencial?¿Tiene solución la ecuación 2^x=0? Y si en vez de 2 ponemos cualquier otro número? d) ¿Cuál sería la solución de cualquier inecuación de la forma a^x>0? ¿Y si fuese a^x < 0? e) Si 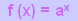, ¿Quién sería el dominio
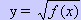de  ]?¿Y el de 1/f(x)?f)¿Qué punto tienen en común todas las gráficas de funciones exponenciales? g)¿Cuando es creciente una función exponencial?¿Y decreciente? |
|||||||||||||||||
Vamos ahora a estudiar la gráfica de la función logarítmica y = log a(x), en donde a debe de ser positiva y distinta de 1. a)En primer lugar, vamos a fijarnos en la forma de la función cuando vamos haciendo con el pulsador que el valor de a aumente. Describe la gráfica de la función logarítmica para a>1:Dominio, recorrido, monotonía y continuidad Haz una tabla de valores en tu cuaderno,como la que te indicamos aqui, para el caso en que a = 2, es decir de la función y= log2 (x)
b) Vamos ahora a hacer lo mismo que en el apartado anterior, pero ahora con el valor de a comprendido entre 0 y 1 .Describe como hemos indicado todas estas gráficas. |
|||||||||||||||
| Haremos
ahora en el cuaderno una tabla de la función logarítmica con base 1/2.
¿Puedes tomar otra vez como referencia la tabla sugerida en
el
apartado anterior? c)¿Cuál es el dominio de la función logarítmica para cualquier base?¿Cuáles son los números de los cuales puedo calcular el logaritmo? ¿Qué tendría que hacer para calcular el dominio de la función log(x-2)?¿Se parece al dominio de alguna otra función que hayamos estudiado en esta unidad? d) Todas las funciones logarítmicas tienen un punto en común,¿cuál es? e) En el caso en que a>1, ¿Qué números tienen logaritmo positivo?¿Como sería la gráfica del valor absoluto de log(x)?¿Y si a>1 ? »Si quieres ver la gráfica de esta función pon el pulsador en 1 f) Compara las tablas de valores de la función exponencial y logarítmica de base 2.¿Tienen alguna relación? ¿Como crees que seran graficamente una con respecto a la otra? Puedes comprobar, poniendo el pulsador en 2, que son simétricas con respecto a la recta y = x. Esto les ocurre porque son funciones inversas.Lo que en la exponencial es variable independiente, en la logarítmica es variable dependiente y viceversa. |
|||||||||||||||
| Carmen Paz Crespo , 2009 página anterior |
