If we expand the brackets of the equation (x-h)²+(y-k)²=r² and bring everything over to one side we get: x²+y²-2hx-2ky+h²+k²-r²=0. This suggests that any equation of the form: x²+y²+dx+ey+f=0 is the equation of a circle whose centre is h=-d/2, k=-e/2 and radius is r²=(d²/4+e²/4)-f. Therefore, whenever d²+e²-4f>0 we get the equation x²+y²+dx+ey+f=0 which is the equation of a circle.

Note:
    Equations of the form ax²+ay²+mx+ny+p=0 have the same solutions as those divided by a; in other words,  those of the form x²+y²+dx+ey+f=0.
Therefore, every circle ax²+ay²+mx+ny+p=0 can also be expressed in the form: x²+y²+dx+ey+f=0 and is always a circle when m²+n²-4pa>0.

The following applet allows us to change the parameter d, e and f and see the corresponding circle which is drawn. The three parameters should always satisfy the following condition: d²+e²-4f>0

14.- If the centre is on the X-axis which parameter in the general equation is 0? When is the centre located on the Y-axis? Draw various circles to check the hypothesis.

15.- Change the parameters to draw circles which pass through the origin of coordinates. What is special about equations of circles which go through the origin?

There are an infinite number of circles which can go through points A and B. If we take the perpendicular bisector of the line which joins these points we can see that any circle whose centre is located on this perpendicular bisector and goes through one of the points (A or B) automatically passes through the other.

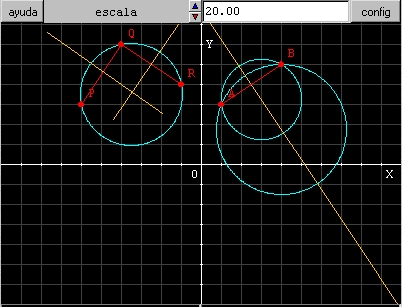If we have three points P, Q and R, which are not in a straight line, the perpendicular bisectors of lines PQ and QR intersect at a point. This point is the centre of the circle which goes through points P, Q and R as it is the point which is equidistant from P, Q and R. Look at the diagram.

If the three points are in a straight line their perpendicular bisectors are parallel and so we can't find a point equidistant from the three.

The diagram shows how to find the centre of a circle which goes through three given points, which are not in a straight line. We can also see that an infinite number of circles can be drawn going through given two points.

As we have already said, we cannot find a circle through three points if the points are in a straight line. We can, however, if the points are not in line. The graph gives enough information to obtain the values for h, k and r after first doing some workings out.

16.- Write the values of the parameters of the circle which goes through points P, Q and R. You will probably need to do some workings out in your exercise book.