
Casos especiales II.
 |
Propiedades de los límites: Casos especiales II. |
| Análisis. | |
| Cociente de un límite finito no nulo entre un límite igual a cero. | |
|
"Sean f y g dos funciones: f con límite finito en el punto a (al que llamaremos b y supondremos mayor que cero) y g con límite cero en a. Entonces la función f/g no está acotada en ningún entorno del punto a".
Es decir
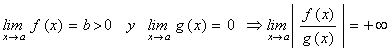
Suele decirse en este caso que el límite del cociente es infinito, sin embargo eso sólo podemos asegurarlo en valor absoluto, como se indica en la expresión anterior. De hecho pueden darse cuatro situaciones diferentes que se muestran en los ejemplos siguientes: |
|
Haz que la x tome valores próximos al punto a, tanto por la izquierda como por la derecha y observa qué sucede con f(x)/g(x). En este ejemplo el límite cuando x tiende al punto a de f(x)/g(x) es más infinito. |
Haz que la x tome valores próximos al punto a, tanto por la izquierda como por la derecha y observa qué sucede con f(x)/g(x). En este ejemplo el límite cuando x tiende al punto a de f(x)/g(x) es menos infinito. |
|
Haz que la x tome valores próximos al punto a, tanto por la izquierda como por la derecha y observa qué sucede con f(x)/g(x). En este ejemplo el límite de f(x)/g(x) cuando x tiende al punto a por la derecha es más infinito y por la izquierda es menos infinito. |
Haz que la x tome valores próximos al punto a, tanto por la izquierda como por la derecha y observa qué sucede con f(x)/g(x). En este ejemplo el límite de f(x)/g(x) cuando x tiende al punto a por la izquierda es más infinito y por la derecha es menos infinito. |
|
Ejercicios.
¿Cuál es la razón de que se produzcan estos cuatro casos? ¿Qué sucederá en el caso de que b sea negativo? Razona las respuestas.
|
| José Luis Alonso Borrego | ||
 |
||
| Ministerio de Educación, Cultura y Deporte. Año 2001 | ||
![]()
Los contenidos de esta unidad didáctica están bajo una licencia de Creative Commons si no se indica lo contrario.