INTEGRACIÓN INMEDIATA II
Análisis
1. FUNCIONES LOGARÍTMICAS
La integral indefinida de la función f(x)=1/x es logaritmo.gif (1165 bytes)

1.- Demuestra la relación precedente.

2.- Generaliza una fórmula para calcular integrales indefinidas, de tipo logarítmico, donde el denominador sea una función a su vez de x.

logaritmica2.gif (1323 bytes)

3.- Calcula las siguientes integrales

  1. log1.gif (1167 bytes)

  2. log2.gif (1224 bytes)
3.log3.gif (1077 bytes)    Indicación: Aunque estas integrales no tengan, a primera vista apariencia de logarítmicas, lo son.
2. FUNCIONES EXPONENCIALES
La integral indefinida de la función f(x)=ex es ella misma más la correspondiente constante de integración. Si la base no es el número e entonces 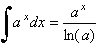expa.gif (1142 bytes).
4.- Demuestra las relaciones descritas anteriormente.
expe.gif (1224 bytes)

expagen.gif (1318 bytes)
Las funciones exponenciales de base el número e se obtienen cuando el parámetro base e toma el valor 1. Si este parámetro toma el valor 0, la base que se considera en la escena es el número que aparece en el parámetro base#e
5.- Calcula las siguientes integrales:
  1. exponen1.gif (1073 bytes)
  2. exponen2.gif (1040 bytes)
3. FUNCIONES TRIGONOMÉTRICAS
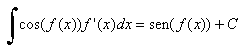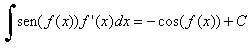La integral indefinida de la función f(x)=cos(x) es la familia de funciones FC(x)=sen(x)+C y la de la función g(x)=sen(x) es GC(x)=-cos(x)+C. En general, coseno.gif (1409 bytes)yseno.gif (1412 bytes)
El parámetro opción cambia la función coseno por la función seno.

6.- Calcula las siguientes integrales indefinidas

  1. trigo1.gif (1101 bytes)
  2.   trigo2.gif (1159 bytes)
Enrique Martínez Arcos
Ministerio de Educación, Cultura y Deporte. Año 2001

Licencia de Creative Commons
Los contenidos de esta unidad didáctica están bajo una licencia de Creative Commons si no se indica lo contrario.