

Dado un triángulo ABC cualquiera, calculamos:
CASO I |
Medianas |
CASO II |
|
CASO III |
|
CASO IV |
La Altura de un triángulo ABC, relativa al vértice A, es la recta perpendicular al lado BC y que pasa por A.
| Sea el triángulo ABC: | |||
| Vértices: | A(A.x,A.y) | B(B.x,B.y) | C(C.x,C.y) |
Posiciona el triángulo en el plano cartesiano, utilizando la escena:
Cálculo de la altura:

| Pendiente de BC: | 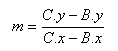 |
| Pendiente de la recta perpendicular a BC: | 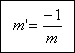 |
| Ec de la altura, recta que pasa por A y de pendiente m': |
EJERCICIOS
1.-Calcula las pendientes de las rectas que contienen a los lados del triángulo de vértices A(2,1), B(1,2) yC(3,3)
2.-Calcula las pendientes de la altura relativa al lado BC, al lado AC y al lado AB.
3.- Calcula las ecuaciones de las alturas.
4.-Resuelve el sistema de ecuaciones formado con dos ecuaciones de alturas, para obtener las coordenadas del Ortocentro.
5.- Comprueba los resultados en la escena.
Autora: MĒ del Carmen Herrero de Evan
| Ministerio de Educación, Cultura y Deporte. Año 2001 | ||