| FUNCIONES DE PROPORCIONALIDAD INVERSA | |
| Análisis | |
| 3.2. Funciones de la forma y=k/x-a +b | |
|
|
8.-Ahora modifica el valor del parámetro b y responde en tu
cuaderno de trabajo: ¿Cómo cambia la gráfica de la función según los distintos valores de b? 9.-Con los valores de los parámetros k, a y b adecuados, dibuja con la aplicación la gráfica de las siguientes funciones:
10.- Copia en tu cuaderno de trabajo la definición y gráfica de las funciones anteriores, y para cada una de ellas indica su dominio y recorrido, si es creciente o decreciente y las ecuaciones de sus asíntotas. |
11.- A la vista de todo lo anterior responde en tu cuaderno de trabajo: ¿En qué se parecen y en qué se diferencian, es decir, qué relación hay entre las gráficas de las funciones siguientes? 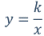
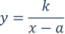
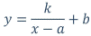 |
|
| 3.3. Cocientes de polinomios de primer grado | ||
En la siguiente escena podemos dibujar las gráficas de las funciones de la forma: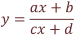 Veremos qué relación hay entre estas funciones y las que estudiamos anteriormente. |
||
|
|
12.- En la escena se ha introducido la gráfica de la función: 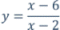 ¿La gráfica parece una hipérbola? ¿Cuál es el dominio de la función? Observa la gráfica, ¿cuál es el recorrido de la función? Modifica la definición de la función (en la parte izquierda inferior de la escena) para ver más ejemplos de funciones con la forma: 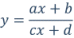
|
|
13.-
En tu cuaderno de trabajo realiza la división (x-6):(x-2) y verifica
que el cociente es 1 y el resto -4. Por lo tanto se verifica que: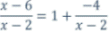 y podemos escribir la función en la forma: 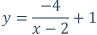 14.- Con los valores de los parámetros k, a y b adecuados, dibuja la gráfica de la función anterior y verifica que coincide con la gráfica de 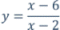 | ||
Las gráficas de todas la funciones de la forma: 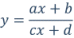 (cocientes de polinomios de primer grado) también son hipérbolas. |
||
 |
 |
 |
||||
| Cecilia Tosar Escuder | ||
 |
||
| Ministerio de Educación, Cultura y Deporte. Año 2012 | ||

Los
contenidos de esta unidad didáctica están bajo una licencia
de Creative Commons si no se indica lo contrario.