PROBLÈMES D'OPTIMISATION (I)

	DÉRIVÉES. APPLICATIONS. OPTIMISATION
	Analyse

8.- PROBLÈMES D'OPTIMISATION (I)
LA BOÎTE
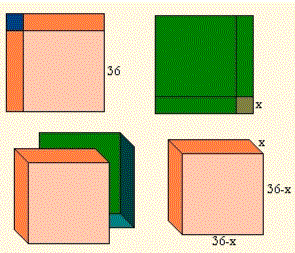	*Nous avons deux pièces carrées de 36 cm de côté. Nous coupons à chacune d'elles un coin carré de côté x, nous doublons les bords, pour unir les deux pièces et former une boîte.* *Combien doit-il coûter x, le côté du carré que nous coupons, pour que le volume de la boîte soit le maximum?* La fonction qui nous donne le volume de la boîte sera: *V=x(36-x)²* Où le *domaine* de la fonction sera 0<36 puisque le carré que nous coupons ne peut pas être plus grand que la pièce accomplie.
La manière de résoudre ce problème change complètement si nous le faisons en calculant, ou si nous le faisons avec Descartes.

a) AVEC DESCARTES

Esta unidad interactiva requiere la máquina virtual de Java J2RE.

Pour pouvoir voir mieux la fonction, nous avons changé les unités à dm, de manière que la fonction représentée dans la scène soit:

V=x(3.6-x)²

Et pourtant leur domaine est 0<3.6

Le paràmetre a, représente les différentes valeurs que nous pourrons donner à x.

Le paràmetre fonction prend seulement deux valeurs, 0 et 1. S'il coûte 0 nous verrons la fonction Volume, et si coûte 1 nous verrons la fonction dérivée.

Le point jaune sera sur la fonction Volume si le paràmetre fonction=0, et il sera sur la fonction dérivée si fonction=1.

Découvrez dans cette scène quel est la valeur de x qui fait maxime la fonction Volume dans l'intervalle (0,3.6), et quelle est cette valeur maximale.

b) SANS DESCARTES

Il faut découvrir le maximum absolu de la fonction V=x(3.6-x)² dans l'intervalle (0,3.6).

Le maximum absolu d'une fonction continue, est dans le maximum relatif (f '(a)=0) ou dans les extrêmes de l'intervalle.

Nous trouvons la fonction dérivée, nous découvrons les valeurs de x qui la font zéro, c'est x=1.2, et x=3.6 (celui-ci ne nous sert pas puisque 0<3.6).

Maitenant nous calculons la valeur de la fonction en x=1.2 et dans les extrêmes de l'intervalle:

f(0)=0, f(1.2)=6.91, f(3.6)=0

En conséquence le maximum de la fonction s'obtient par x=1.2, f(1.2)=1.2*2.42=6.91

Est-ce que c'était le même que nous avions obtenu dans la scène?

TRIANGLES RECTANGLES

Esta unidad interactiva requiere la máquina virtual de Java J2RE.

Parmi tous les triangles rectangles les cathètes desquels additionnent 10cm, trouvez les dimensions de celui qui a une aire maximale.

Dans cette scène tu as représenté les triangles qui accomplissent que la somme de leurs cathètes est 10.

Déplacez avec la souris le sommet B, et tu pourras obtenir différents triangles avec les mêmes conditions.

D'autre part, c'est représentée la fonction aire, prenant comme variable la cathète x.

Sans bouger le point B tu pourras chercher la solution du problème.

Quel est le domaine de la fonction aire dans ce problème?

	Ángela Núñez Castaín Version française: Rocío Oliver Sánchez, Carme Llaberia Azcón, Joan Carles Fiol Colomar

	Ministerio de Educación, Cultura y Deporte. Année 2011

Sauf indication contraire, les contenus de cette unité sont sous une licence de Creative Commons.