Las "epicicloides acortadas" (epitrocoides cortos) son curvas que se pueden obtener con un Spirograph, haciendo rodar un círculo exterior sobre otro círculo, que permanece fijo, colocando un bolígrafo en cualquier punto P (agujero) del círculo que rueda. 

Las "epicicloides alargadas" (epitrocoides largos) son curvas generadas de modo análogo a las epitrocoides cortas pero en las que el punto P es un punto vinculado al círculo que rueda pero fuera del disco

La ecuación general de las epicicloides alargadas se obtiene de análoga forma que la de la acortada, solamente tenemos que tener presente que a>r

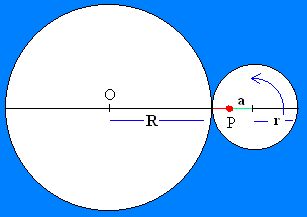
En la figura se muestra la geometría de la epitrocoide corto (color verde) en la cual un círculo de radio r rueda por el exterior de un círculo fijo de radio R.

Actividad 5:

1. Trata de encontrar su ecuación observando la escena.

2. Comprueba, pulsando las flechas del botón "Demo"  que tu demostración es correcta. 

• Cambia los valores de los controles y observa la colocación inicial de los puntos respecto a la circunferencia de radio r.

• Con las flechas del control ángulo verás como se generan las curvas.

• Observa la epicicloide (color blanco) y las epitrocoides  (color verde) que se obtienen con los valores de R y r considerados.

• Observa en la parte superior, en el color correspondiente a la gráfica, el tipo de curva que describe el punto considerado. Observa a su derecha el nombre de algunos casos especiales de curvas.

• Si deseas representar otra gráfica te recomendamos que utilices el botón iniciar y cambies los valores de los controles.

Cambia el valor de zoom para visualizar bien las curvas.

1. Si R=r=a se obtiene la curva llamada Cardioide. Compruébalo.

2. Si R=2r y r=a se obtiene la curva llamada Nefroide o epicicloide de Huygens (S. XVII)

3. Si a=0 ¿Qué ocurre?

4. Practica los valores de la tabla y experimenta con otros valores