Continuity of functions:
An intuitive approach.
2nd year of post-compulsory secondary education.
 
A look at the functions y = sgn(x) and y = 1/x.

Look at the window below. The parameter m can have the following two values:1 or 2. Select each value and look at the different functions given.

If you select m=1 you will see the curve of the function y = sgn(x) :

The function above is not defined at x=0.

If you select m=2 you will see the curve of the function y = 1/x

If you change the B.x parameter you will see that point B moves over the curve. You can also move B by dragging the red and yellow point with the mouse along the X-axis.

Make the parameter m equal to 1. The function is y = sgn(x) :

1.- Use the mouse to drag the red and yellow button over the curve. What happens when the value is 0? Select values for the parameter B.x which are close to zero on both the left-hand side (less than zero) and the right-hand side (more than zero). You should notice that as the point passes through 0, the Y-coordinate of point B jumps from (-1) to (1).

2.- What do you think?: Is this function continuous or discontinuous? Explain your answer.

Now make the parameter m equal to 2. The function is y = 1/x :

3.- Move over the graph of the function by using the mouse to drag the red and yellow button along the X-axis. What happens when the value is 0? Select values for the parameter B.x which are very close to zero. If B = (B.x, B.y), the coordinates for B on the graph are given when the x-coordinate B.x is very close to zero on both the right and left-hand side. What are the values of the function (B.y)? What is the value of the function when B.x = 0?

4.- Do you think that this function is continuous or discontinuous? Explain your answer.

A look at the functions 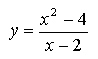and .

Let's first focus on the function

You can move over the curve of the function as before, by dragging the red and yellow point along the X-axis with the mouse, or by changing the parameter B.x.

5.- What happens to B when B.x = 2? What is its image (the value of the function)? What are the values of the function when the value of B is close to 2 both to the left and the right?

6.- Do you think that this function is continuous? Explain your answer.

Now, let's take a look at the function

You can move over the curve of the function as before, by dragging the red and yellow point along the X-axis with the mouse, or by changing the parameter B.x.

7.- What happens when B.x < -5 or B.x = -5? Is the function continuous? Explain your answer.

A look at the function y = log(x).

Note that the function y = log (x) does not exist when x<0 or x=0 What is the behaviour of the function for the other values of x?

We are going to focus on its continuity at point A. You can select this point by changing the parameter A.x, which is the x-coordinate of A.

Once A has been selected, move point P over the curve by dragging it with the mouse or by changing the values of the parameter P.x, which is the x-coordinate of P.

9.- Do you think that the function is continuous at point A? Explain your answer.

       
           
  Belén Pérez Zurdo.
 
Spanish Ministry of Education. Year 2001