L'enveloppe : une méthode magique (1)

Celle du triangle équilatéral (animée en flash) L'enveloppe carrée ou rectangulaire L'enveloppe triangle rectangle isocèle ou demi-carré L'enveloppe demi-triangle équilatéral (animée en flash) Pourquoi il n'en existe pas d'autre... L'écureuil, enveloppe avec tétraèdre En savoir un peu plus sur les pavages Les 17 types de pavage

Comment fabriquer des motifs qui s'emboîtent parfaitement comme un puzzle pour remplir le plan ?
Découvrons ici la méthode magique et surprenante de l'enveloppe. Elle permet d'obtenir de jolies formes pavantes. Le motif obtenu est souvent inattendu. Aussi est-il utile de concilier cette procédure avec celle du découper coller.

Le principe est simple :

Choisir deux morceaux de papier superposables ayant une forme spécifique (nous verrons que cette forme n'est pas quelconque).
Scotcher ces deux morceaux pour former une enveloppe fermée.
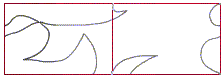
Choisir un point quelconque sur l'une des faces et tracer des courbes le reliant à chacun des sommets de la figure en passant devant ou derrière l'enveloppe.
Impératif : les lignes ne doivent pas se couper.
Découper ensuite sur une seule épaisseur de papier en suivant la ligne. (Prendre des ciseaux pointus ;o)
En dépliant on obtient une figure pavante.
Ci-dessous nous allons découvrir les formes possibles et voir quelques exemples animés.

Pour profiter au maximum de cette page appuie sur la touche F11
Si les boutons ne réagissent pas, télécharger ici la version Flash 5  

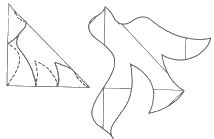
1- Enveloppe en forme de triangle équilatéral.

On place l'un contre l'autre deux triangles équilatéraux identiques. On les colle avec du scotch sur les 3 côtés. Ensuite on ne découpera qu'une face à la fois. Sur le plan pratique, il vaut mieux ne souder que deux côtés d'emblée, commencer à découper, puis scotcher le troisième côté.

On choisit un point sur l'un des deux triangles. De ce point on trace un chemin (qui peut passer en arrière) vers chacun des trois sommets du triangle. Ce chemin peut passer par la face arrière. Attention les trois chemins ne doivent pas se couper entre eux. On découpe sur la ligne une seule épaisseur à la fois.
Voici un exemple animé. 

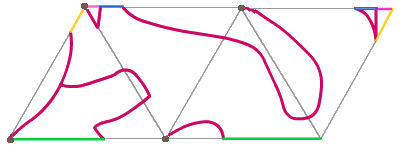
Avec cette enveloppe, le pavage se construit avec des translations et des rotations d'un tiers de tour. Le chinois du jeu puzzle a été construit par cette méthode, voici le recto et le verso de l'enveloppe :
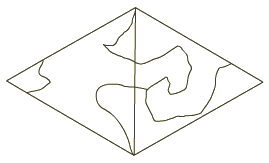
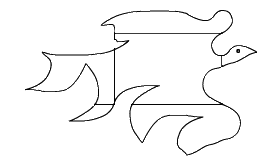
Le bonhomme de droite est obtenu avec une telle enveloppe. En pliant ce bonhomme toujours dans le même sens sur les segments, on retrouve l'enveloppe de départ.

2- Enveloppe carrée ou rectangulaire

On place l'un contre l'autre deux carrés ou deux rectangles.   On choisit un point sur l'une des deux faces. De ce point on trace un chemin vers chacun des quatre sommets de la figure. Ce chemin peut passer par la face arrière. Les quatre chemins ne doivent pas se couper entre eux. Ci-dessous les oiseaux d'Escher.
Voici le recto et le verso de l'enveloppe, scotcher les deux rectangles sur les côtés puis découper.
Avec cette enveloppe, le pavage utilise des translations et des rotations d'un demi-tour.

3- Enveloppe en forme de triangle rectangle isocèle ou demi-carré

On place l'un contre l'autre deux triangles rectangles isocèles.   On choisit un point sur l'une des deux faces. De ce point on trace un chemin vers chacun des trois sommets de la figure. Ce chemin peut passer par la face arrière. Les trois chemins ne doivent pas se couper entre eux. La perruche peut aussi être réalisée à partir d'un triangle rectangle isocèle. Avec cette enveloppe, le pavage utilise des translations, des rotations d'un demi-tour et des rotations d'un quart de tour.

4- Enveloppe en forme de demi triangle équilatéral

On procède de la même façon que ci-dessus avec deux moitiés de triangle équilatéral. Il suffit en réalité de plier un triangle équilatéral sur sur l'une de ses hauteurs.

Le pacman peut être obtenu avec avec une telle enveloppe.  Le pavage utilise des translations, des rotations d'un demi-tour, des rotations d'un tiers de tours et des rotations d'un sixième de tour. La pantoufle de vair peut également s'obtenir avec une enveloppe demi-équilatérale .

5- Il n'existe pas d'autre forme d'enveloppe plane...  

Nous allons voir que seules cinq formes d'enveloppes existent :
le carré, le rectangle, le triangle équilatéral, le triangle rectangle isocèle et enfin le triangle demi-équilatéral.
En effet, les différentes rotations ont pour centres les sommets de l'enveloppe.
On voit aussi qu'au cours du pavage, la rotation du motif autour d'un sommet A de l'enveloppe sera d'un angle dont la mesure est le double de celui de l'angle a en le sommet A de la figure. Ce sera donc 2a .
Maintenant, il faut qu'après un certain nombre de rotations d'angle 2a, on revienne exactement au point de départ, donc que l'on ait effectué un tour complet de 360°.
            Ainsi (2a) doit diviser 360° donc être de la forme 360 /n avec n entier naturel
            ou encore a est de la forme 180/n.
Si l'enveloppe est triangulaire, alors il faudra que la somme des 3 angles soit de 180°.
Si l'enveloppe est un quadrilatère, alors il faudra que la somme des 4 angles soit de 360°.
Si l'enveloppe est pentagonale il faudra que la somme des 4 angles soit de 540°.
Et ainsi de suite...

6- L'écureuil : une enveloppe en dimension 3, le tétraèdre

Le motif de l'écureuil peut s'obtenir avec une enveloppe en dimension 3, un berlingot c'est à dire un tétraèdre régulier.
On construit le patron d'un tétraèdre avec 4 triangles équilatéraux comme ci-dessous. On dessine alors les courbes indiquées, en veillant à ce que les segments colorés en jaune, rose bleu et verts aient bien même longueur. On scotche alors les faces pour construire le tétraèdre. Il suffit alors de découper chaque face selon la courbe rouge. En aplatissant on obtient un écureuil pavant avec des rotations d'un demi-tour.
Les 4 sommets du tétraèdre sont alors les centres de rotation du pavage, que nous avons pu observer dans le puzzle des écureuils.

7- En savoir un peu plus sur les pavages

Un quadrilatère quelconque convexe ou non pave (chaque quadrilatère cache un parallélogramme paveur qui joint les milieux de ses côtés) , ce n'est pas le cas du pentagone. Les formes régulières ou non ne pavent donc pas systématiquement.

Les différentes méthodes vues :

-couper-coller, -déformation, -enveloppe, -cône réalisé avec un triangle isocèle ayant un angle de 120° , enroulé, collé puis découpé le long d'un tracé allant du bas du cône vers le sommet.

nous donnent de jolis motifs paveurs.

Le cristallographe et mathématicien russe Fedorov a montré en 1891 (Université de Saint-Petersbourg), qu'il n'existe que 17 types de pavages du plan. Ces types sont classés suivant l'agencement des rotations et des symétries qu'on peut y trouver.
Les arabes ont développé de très beaux pavages géométriques. En effet, ils ne devaient pas représenter Allah et ont puisé leur inspiration dans la géométrie. Ils ont créé en Andalousie de merveilleux chefs d'oeuvre pour décorer palais et mosquées en utilisant toutes les dispositions possibles. Ce sont de vrais précurseurs dans le domaine des pavages.
Le graveur hollandais Maurits Cornelius Escher a créé de nombreux pavages utilisant des animaux ou des personnages étranges. Nous en avons vu quelques uns.
Raoul Raba sculpteur contemporain est devenu un maître ès-pavages (1).
En 1974, le mathématicien Penrose trouve des formes simples donnant des pavages non-périodiques. 10 ans plus tard des chimistes découvrent les "quasi-cristaux" (assemblages par 5) impossibles dans un cristal normal. Quelques 25 ans plus tard ces quasi-cristaux tapissent le fond des poëles à frire anti-adhésives... Les pavages n'ont pas qu'un intérêt esthétique et mathématique ;o) 

 

 

(1)  Voir aussi RAOUL RABA Les secrets des pavages editions Sciences & Images
A.DELEDICQ R.RABA Le MONDE DES PAVAGES ACL - éditions du Kangourou